Inverse to a Curious Partition Problem, Correct Solution

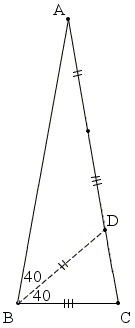
Inverse to a Curious Partition Problem
Correct Solution

In ΔABC, ∠B = 80°. The bisector of angle B meets AC in D such that AD = BC + BD. Find angle C.

The first attempt at the problem has been found to contain a mistake - making an assumption that is equivalent to the statement one has to prove. Here's a correct

Solution

In ΔABC, ∠B = 80°. The bisector of angle B meets AC in D such that AD = BC + BD. Find angle C.

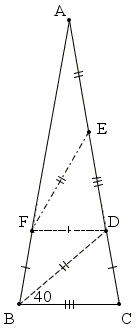
Let F on AB be such that DF||BC. Then

∠BDF = ∠CBD = ∠DBF = 40°,

making, in particular, ΔBDF isosceles:

BF = DF.

Now there are three possibilities: CD = BF, CD < BF, and CD > BF. In the first case, there is nothing to prove. The trapezoid BCDF is isosceles so that ∠BCD = ∠CBF = 80°.

Let's denote ∠BCD = γ. If CD < BF, then γ > 80°; otherwise, if CD > BF, then γ < 80°.

For both cases we shall define a point E on where ∠DEF = 40°. This choice makes triangles BCD and EDF similar, because also ∠EDF = ∠BCD.

Assume, CD < BF. Then also CD < DF. All sides of Δ EDF are greater than their counterparts in ΔBCD. In particular, EF > BD and also DE > BC. Since AD = BC + BD, AE < BD < EF. Thus in ΔAEF, ∠AFE < ∠EAF. Since the sum of the two angles is 40°, ∠EAF > 20°.

However, the assumption CD < BF implies that γ > 80° and we get a contradiction since angles in ΔABC add to more than 180°.

The case CD > BF similarly leads to a contradiction.

72264314

Inverse to a Curious Partition Problem Correct Solution

Inverse to a Curious Partition Problem
Correct Solution