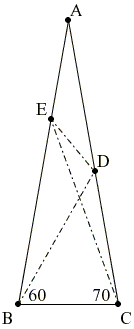
The 80-80-20 Triangle Problem, 60-70 Variant, Solution #1

Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 60°. Point E is on side AB such that ∠BCE = 70°. Find the measure of ∠CED.

Solution

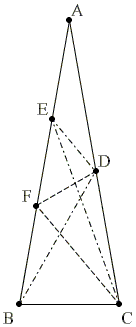
The solution is by Philippe Fondanaiche.

Find F on AB with ∠BCF = 50°. This brings us into the classical framework so that we, for example, know that ∠BDF = 30°.

In ΔBDF, ∠DBF = 20° and ∠BFD = 130°. In ΔCFE, ∠ECF = 20°, ∠CEF = 30° such that the two triangles are similar:

(1)	DF / EF = BF / CF

Since ∠BFC = 50°, ΔBCF is isosceles and BF = BC. Also, ∠DFE = 50°. With (1), this tells us that triangles BCF and DFE are similar, so that the latter is also isosceles and DF = DE. Hence, ∠DEF = 50° and

∠CED = ∠DEF - ∠CEF = 50° - 30° = 20°.

72202357