Proofs of the Pythagorean Theorem via Heron's Formula II

I was reminded of this proof by José Antônio Fabiano Mendes from Rio de Janeiro, Brazil. It appears as the algebraic proof 107 in Loomis' collection.

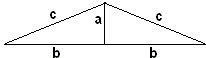
Pythagorean theorem via Heron's formula, #1

Join two copies of the base right triangle with legs $a,$ $b$ and hypotenuse $c$ as shown in the diagram. The result is an isosceles triangle with side lengths of $2b,$ $c$, $c$ and area $S = ab,$ obviously. To this triangle we apply Heron's formula. With the semiperimeter $p = b + c,$ we have

$S^{2} = (b + c) b^{2} (c - b).$

Substituting $S^{2} = (ab)^{2}$ and dividing by $b^{2}$ we obtain

$a^{2} = c^{2} - b^{2}.$

This is indeed a much shorter application of Heron's formula than proof #23.

If the length of the derivation is of no concern, note that Heron's formula extension, i.e. Brahmagupta's formula for cyclic quadrilaterals could be used in proof #52; for an isosceles trapezoid is cyclic. To apply Brahmagupta's formula we'll have to use the Socratic version of the Pythagorean theorem as was done in proof #64. The result is lengthier than proof #52 but, otherwise, is much along the lines of the above derivation.

Loomis mentions that Versluys attributes the proof to J. J. Posthumus.

John Molokach found a different way of using Heron's formula. Instead of combining two triangles into an isosceles one, he splits the given triangle into two isosceles:

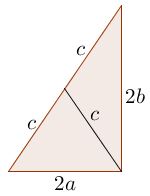
Pythagorean theorem via Heron's formula, #2

Now, both isosceles triangles have area equal to $S=ab.$ Heron's formula may apply to either. E.g., for the lower one:

$ab=\sqrt{(a+c)\cdot a\cdot a\cdot (c-a)},$

such that $a^{2}b^{2}=a^{2}(c^{2}-a^{2})$ and, subsequently, $b^{2}=c^{2}-a^{2}.$

References

E. S. Loomis, The Pythagorean Proposition, NCTM, 1968

71931854