An Identity in a Regular Heptagon

A regular heptagon - a polygon with 7 sides and 7 vertices - is mostly known for the ancient construction conundrum - to construct a regular heptagon using only straightedge and compass. As is now well known, the problem has no solution. Which of course does not mean that the shape has no special and unexpected properties. One such is described in R. Vakil's book (p. 100). (He mentions that the problem adorns the business card of Richard Rusczyk, the founder of the artofproblemsolving.com site.)

Let A, B, C, D be consecutive vertices of a regular heptagon. Define X to be the intersection of AC and BD.

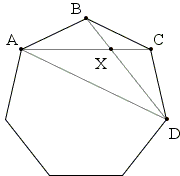Prove that AB + AX = AD.

One solution can be found at Richard's site, another below.

Reference

1. R. Vakil, A Mathematical Mosaic, Brendan Kelly Publishing, 2008 (Expanded Edition)

|Contact| |Front page| |Contents| |Geometry| |Store|

Let A, B, C, D be consecutive vertices of a regular heptagon. Define X to be the intersection of AC and BD.

Prove that AB + AX = AD.

Solution

First of all observe that, as every regular polygon, the regular heptagon is cyclic, with every side subtending 180°/7 inscribed angles. In particular, angles BAC, CAD, and ADB are 180°/7. (This is shown in the diagram bellow where some angles are designated as the multiples of 180°/7.)

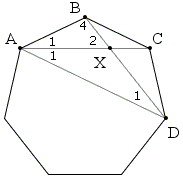ΔAXD is isosceles so that ∠AXD = 5×180°/7, implying ∠AXB = 2×180°/7 and ∠ABX = 4×180°/7. Also, AX = DX.

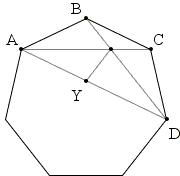
Pick Y on AD such that ∠AXY = 2×180°/7 = ∠AXB.

Since the angles at A are also equal, ΔABX = ΔAYX. In particular, AB = AY.

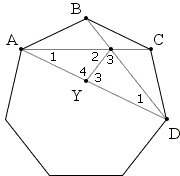In ΔDXY, ∠DXY = ∠DYX = 3×180°/7, making the triangles isosceles such that DX = DY. But we saw that DX = AX. Thus, finally,

|Contact| |Front page| |Contents| |Store| |Geometry|