Pythagorean Theorem: An Algebraic Proof with Three Trapezoids

This page grew out of a discussion at the CTK Exchange started by John Molokach. John came up with a proof of the Pythagorean theorem based on the following diagram:

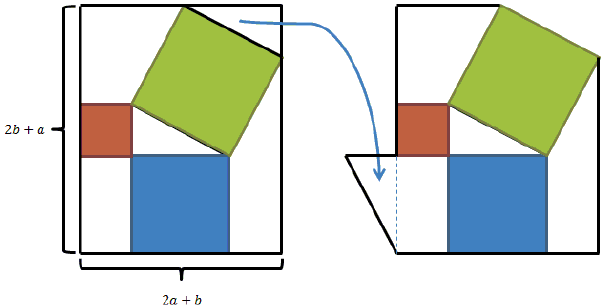
As usual, a and b denote the lengths of the legs (the sides forming the right angle) of a right triangle, c the length of its hypotenuse. On the left, the famous Bride's Chair is embedded into a rectangle whose dimensions are easily seen to be (2b + a) and (2a + b). Thus the rectangle has the area of (2b + a)×(2a + b) = 2a² + 5ab + 2b².

To prove the theorem, John moved one of the triangles as shown in the right part of the diagram. The right part appears to consist of three squares and three trapezoids. As is well known, the area of a trapezoid could be calculated as the product of the average of its bases times its height - the distance between the bases. For all three trapezoids in the diagram, the area of 3ab/2. This leads to the following identity:

Eliminating the ab terms and canceling a² + b² on both sides gives a² + b² = c². It must be noted that the proof does not appear in Loomis' collection.

John has also suggested that with additional modifications the three trapezoids may be made equal, and not just have the same area. The modification is being illustrated below:

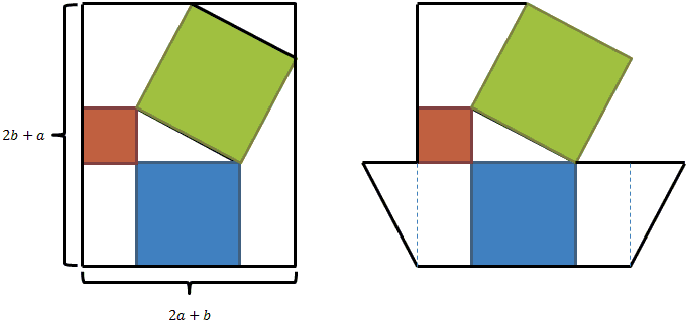
Bui Quang Tuan has remarked that one could apply algebra directly to the left diagram which consists of three squares, a rectangle, two triangles, and two trapezoids, with areas, a², b², c², ab, 2·ab/2, and 2·3ab/2, respectively. Furthermore, the trapezoids could be seen as the unions of a×b rectangles and copies of the original triangle so that two triangles fit into one rectangle. John then expressed this idea in the following diagram:

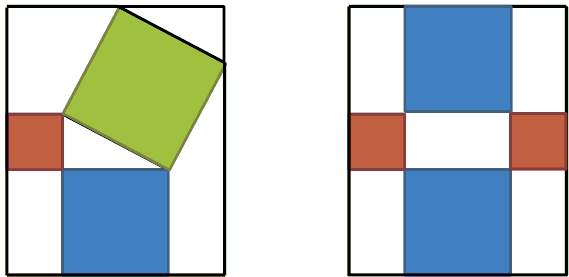
which appears to be a symmetric expansion of another popular proof.

References

1. E. S. Loomis, The Pythagorean Proposition, NCTM, 1968

|Contact| |Front page| |Contents| |Geometry| |Pythagorean Theorem|