An Unusual Generalization of the Pythagorean Theorem, a Variant
This is a variant of Tran Quang Hung's extention of the Pythagorean theorem:
In acute $\Delta ABC,$ $AD,$ $BE,$ $CF$ are the altitudes. Construct squares $BCX_{1}X_{2},$ $BFZZ_1,$ and $CEYY_1$ outside $\Delta ABC.$ Let rectangles $ABZ_{1}Z_2$ and $ACY_{1}Y_{2}$ circumscribe the latter two.
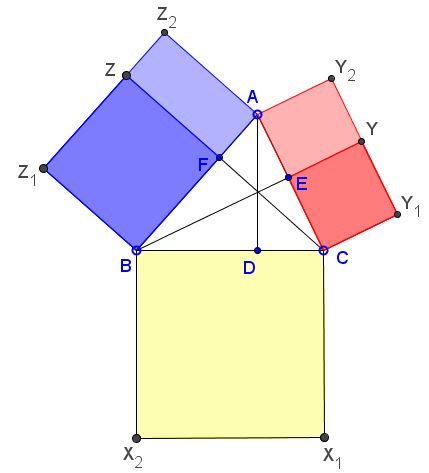
Denote $[X]$ the area of shape $X.$ Then $[BCX_{1}X_{2}]=[ACY_{1}Y_{2}]+[ABZ_{1}Z_2].$
Proof
Circle $(AB)$ an $AB$ as a diameter passes through $D$ and $E.$ Similarly $AC$ passes through $D$ and $F.$
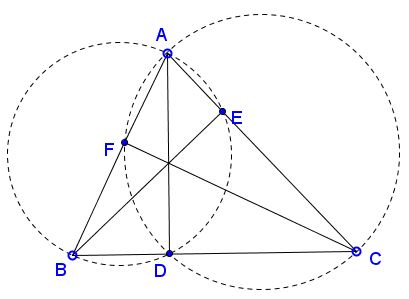
The Power of a point theorem shows that $CD\cdot CB=CE\cdot CA$ and $BD\cdot BC=BF\cdot BA.$ Thus we deduce
$\begin{align}\displaystyle [BCX_{1}X_{2}] &= BC^2\\ &=BC\cdot (DB+DC)\\ &=BD\cdot BC+CD\cdot CB\\ &=BF\cdot BA+CE\cdot CA\\ &=BZ_{1}\cdot BA+CY_{1}\cdot CA\\ &=[ABZ_{1}Z_2]+[ACY_{1}Y_{2}], \end{align}$
as required.
Note that the basic identity $BC^{2}=BF\cdot BA+CE\cdot CA$ is the essence of Proof #102.
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73586709
