An Unusual Generalization of the Pythagorean Theorem

Tran Quang Hung found an extention of the Pythagorean theorem:

In $\Delta ABC,$ $AD,$ $BE,$ $CF,$ are the altitudes. Triangles $BCX,$ $CEY,$ and $BFZ$ outside $\Delta ABC$ are equlateral.

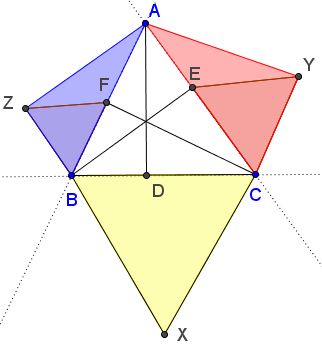
Tran Quang Hung's extension of the Pythagorean theorem

Denote $[X]$ the area of shape $X.$ Then $[\Delta BCX]=[\Delta ACY]+[\Delta ABZ].$

This is a true generalization of the Pythagorean theorem which is obtained when angle at $A$ is right. Moreover, it holds for any triangle. For an acute (as above); when the angle at $A$ is obtuse:

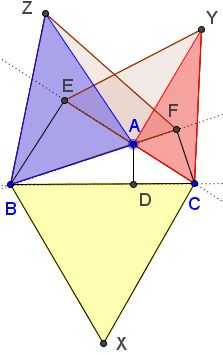
Tran Quang Hung's extension of the Pythagorean theorem, angle A is obtuse

Or even when, say, the angle at $C$ is obtuse.

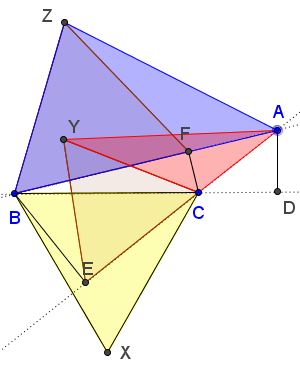
Tran Quang Hung's extension of the Pythagorean theorem, angle C is obtuse

In the latter case, the extended Pythagorean identity should be understood algebraically, viz., $[\Delta BCX]=[\Delta ABZ]-[\Delta ACY].$

Proof

Circle $(AB)$ an $AB$ as a diameter passes through $D$ and $E.$ Similarly $AC$ passes through $D$ and $F.$

Tran Quang Hung's extension of the Pythagorean theorem, proof

The Power of a point theorem shows that $CD\cdot CB=CE\cdot CA$ and $BD\cdot BC=BF\cdot BA.$ Thus we deduce

$\begin{align}\displaystyle \frac{4}{\sqrt3}[\Delta BCX] &= BC^2\\ &=BC\cdot (DB+DC)\\ &=BD\cdot BC+CD\cdot CB\\ &=BF\cdot BA+CE\cdot CA\\ &=\frac{2}{\sqrt3}dist(Z,AB)\cdot BA+\frac{2}{\sqrt3}dist(Y,AC)\cdot CA\\ &=\frac{2}{\sqrt3}(2[\Delta ACY]+2[\Delta ABZ]), \end{align}$

as required.

Note that the basic identity $BC^{2}=BF\cdot BA+CE\cdot CA$ is the essence of Proof #102.

71931714