Pythagoras, with a Nod to the Carpets Theorem

The proofs below are by Tony Foster, III.

Proof 1

This is the simplest of the three and has been submitted last. It is based on the following diagram

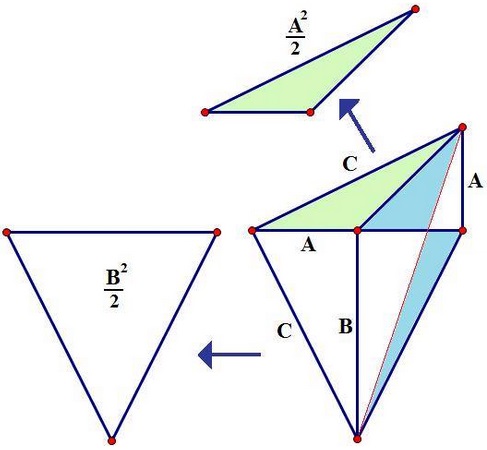
Tony Foster's proof 1

In the diagram, the side length of the triangles are unconventionally denoted by capital letters. The two triangles, one of area $\displaystyle\frac{A^2}{2},$ the other of area $\displaystyle\frac{B^2}{2},$ have been duplicated separately from the main figure. The clue to the proof is twofold: first locate the right isosceles triangle with legs $C$ and then observe that the two blue triangles have the same area. This is a very general property of trapezoids that has been established in the proof of the Carpets Theorem. The diagram leads to the required identity: $\displaystyle\frac{A^2}{2}+\frac{B^2}{2}=\frac{C^2}{2}.$

Proof 2

The second proof is a little more complicated. Note that $\Delta KMO$ is right isosceles with the legs of length $C.$

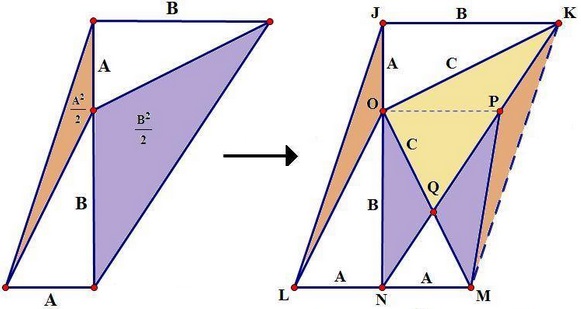
Tony Foster's proof 2

By the property of trapezoids already used in Proof 1, triangles $NOQ$ and $MPQ$ have equal areas. More than that, triangles $JLN$ and $KNM$ have equal areas as are triangles $OLN$ and $PNM$ so that this is also true of the pair $OLN$ and $PNM,$ making the remaining triangles $JLO$ and $KPM$ of equal area. So we have

$\displaystyle\begin{align} \frac{C^2}{2}&=Area(\Delta KOM)\\ &=Area(\Delta KOQ + \Delta MPQ +\Delta KPM)\\ &=Area(\Delta KOQ) + Area(\Delta MPQ) +Area(\Delta KPM)\\ &=Area(\Delta KOQ) + Area(\Delta NOQ) +Area(\Delta JLO)\\ &=Area(\Delta KNO) + frac{A^2}{2}\\ &=\frac{B^2}{2} + \frac{A^2}{2}. \end{align}$

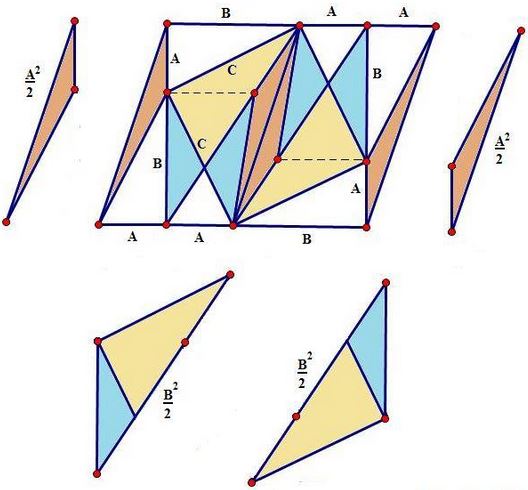
Proof 3

This proof is the symmetric variant of the previous one. It is based on the following diagram

Tony Foster's proof 3

72369892