Parallelogram and Ellipses

Here is a lovely problem from the recently published problem book:

Let \(ABCD\) be a parallelogram in the plane. Describe and sketch the set of all points \(E\) in the plane for which there is an ellipse with the property that the points \(A\), \(B\), \(C\), \(D\), and \(E\) all lie on the ellipse.

Solution

References

M. I. Krusemeyer, G. T. Gilbert, L. C. Larson, A Mathematical Orchard, MAA, 2012, #172

Without loss of generality we may assume that one of the sides of the parallelogram lies on the \(x\)-axis. Then first - in order to convert the parallelogram to a rectangle - apply shear transform parallel to the \(x\)-axis. And then stretch (or squeeze) the rectangle into a square. The two transformations are linear and invertible so that incidence relations between points and lines remain in place and conics convert to conics of the same kind (so that, e.g., ellipses remain ellipses.) Therefore it is sufficient to solve the problem in case of a square. With a change of variables (or an extra linear transform) we may assume to deal with the unit square, with vertices \((0,0)\), \((1, 0)\), \((0,1)\), \((1,1)\). In this case it is easy to explicitly write an equation for a conic through the vertices and point, say, \(E(u,v)\).

Indeed, take for example

\((v^{2} - v)(x^{2} - x) - (u^2-u)(y^{2}-y)=0.\)

First of all, for fixed \(u\) and \(v\), this is a second order equation, so it describes a conic. Second of all, by direct verification we see that point \(E(u,v)\) belongs to the conic. (There are exceptional cases where either \(v^{2} - v= 0\) or \(u^2-u=0\), i.e., where \(E\) lies on the extended sides of the square. On such occasions the conic degenerates, except when \(E\) coincides with one of the vertices of the square, in which case the number of non-degenerate conics through the five (actually four) points is infinite.

In the non-degenerate case, the squares of both \(x\) and \(y\) are present so that the conic is either an ellipse or a hyperbola. Here are the two cases:

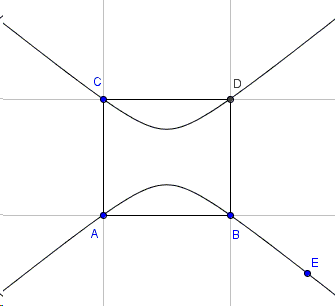
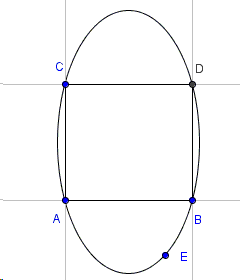
hyperbola through the vertices of a square ellipse through the vertices of a square

Which one it is depends on the sign of the coefficient \(\displaystyle K=\frac{v^{2} - v}{u^2-u}\). When \(K\) is negative, the conic is ellipse, when K is positive, the conic is hyperbola. So the question is when \(\displaystyle K=\frac{v^{2} - v}{u^2-u}\lt 0?\)

For this to happen one of \(v^{2} - v=v(v-1)\) and \(u^{2}-u=u(u-1)\) needs to be negative, the other positive. So that, when one of \(u\) or \(v\) is restricted to the interval \((0,1)\), the other must be outside the interval \([0,1]\). This happens for \(E\) in the darkened half-bands attached to the sides of the unit square:

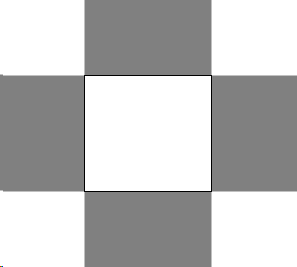
half strips attached to the unit square

What Is Shear Transform?

72187447