This is a truly amazing question. Is it possible to partition the space with circles? In other words, is it possible that 3-space is a union of disjoint circles?

Now, in geometry, because of the properties of inversion, it is often convenient to think of straight lines as circles of infinite radius with center at infinity. If we allow such an interpretation, then the task is easy. We may think of 3-space as being the union of all the planes z = const parallel to the xy-plane. Each of this planes is the union of the circles x² + y² = r² centered at the origin of the plane with all possible radii r > 0, and a point - the origin itself. These points fill the z-axis; and we are done if the latter is thought as a special circle.

On second thought, the preceding construction suggests another solution. If we accept points as being circles of radius 0, we get an even more straightforward partition. Each of the planes z = const is partitioned into circles plus a point.

A plane can also be partitioned into a union of circles plus two points. Any coaxal family of not intersecting circles will do the job. Perhaps there are other approaches that render the question trivial. Is there a nontrivial solution? I.e., is there such a partition of 3-space into circles of non-zero finite radii?

Quite surprisingly, the answer is yes. As a clue, planes and spheres have a lot in common. In particular, a sphere, like a plane, can be partitioned into a union of circles plus two points. Indeed, the two points can be chosen arbitrarily. They need not be the poles, say.

Copyright © 1996-2008 Alexander Bogomolny

Solution

An elegant solution is based on the following diagram.

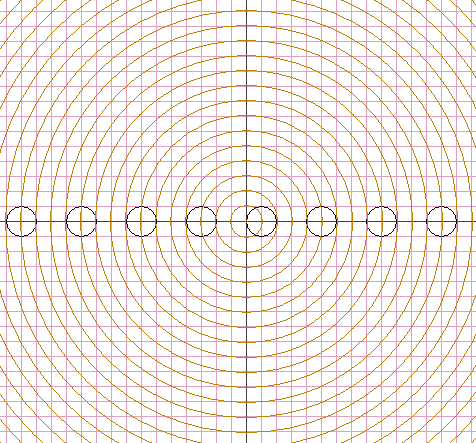
Select an arbitrary unit of measurement and first draw an integer grid in the xy-plane. Next draw (black) circles of radius 1 centered at the points (x, 0), where x = 1 (mod 4). Every sphere centered at the origin (orange circles are cross sections of such spheres by the xy-plane) intersect the union of the black circles in exactly two points (see the diagram.) Each sphere, with the two points out of consideration, can be partitioned into circles, as was mentioned before.

References

1. P. Winkler, Mathematical Puzzles: A Connoisseur's Collection, A K Peters, 2004

Copyright © 1996-2008 Alexander Bogomolny