In 1737 L.Euler published the following formula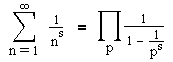

On the left, we sum up the reciprocals of all integers n starting with 1 raised to the real power of s. Such a sum is known in Calculus as an infinite series or just series. Some series are divergent, some convergent. Convergent series are ascribed a unique number known as the sum of a series. On of the first results in the theory of infinite series is to establish that the above series is convergent for all s>1. Thus it has a sum. Euler's formula claims that the same number can be found as an infinite product as expressed on the right. Except that on the right there is one term for every prime number. As was the case with the series, some infinite product diverge, some converge. The one in Euler's formula converges for s>1.

The explanation of the formula starts with the expression for the geometric series (which is an infinite series in its own right, convergent for |q|<1):

For s>1 and integer n, 0<1/n^s<1 which gives

With this we may rewrite Euler's formula in the expanded form

which (convergence questions aside) is almost a reformulation of the fact that every integer can be represented as a product of prime numbers. Picking on the right from between a pair of parentheses a single term and multiplying all of them we'd get a reciprocal of an infinite product:

Unless only a finite number of terms is 1, such a reciprocal is 0 as a product of an infinite number of terms less than, say, 1/2. With only a finite number of terms different from 1 the result is a reciprocal of an integer (raised to the sth power) which, according to Euler's formula, is uniquely defined by its prime components - the Fundamental Theorem of Arithmetic.

References

1. C.Clawson, Mathematical Mysteries, Plenum Press, 1996

|Contact| |Front page| |Contents| |Up|

Copyright © 1996-2018 Alexander Bogomolny

71547433