On Dedekind Cuts

Just before a section where he describes the first of G. Cantor's proofs of the innumerability of the reals which uses the completeness property of the reals, William Dunham in his book The Calculus Gallery (Princeton University Press, 2005, 160-161) observes:

Affirmative answers to this question came from Cantor and, independently, from his friend Richard Dedekind ((1831-1916). Cantor's construction of the reals was based on equivalence classes of Cauchy sequences of rational numbers. Dedekind's approach employed partitions of the rationals into two disjoint classes, the so-called "Dedekind cuts." A thorough discussion of these matters would carry us far afield, for constructing the real numbers from the rationals is a bit esoteric for this book and, truth be told, a bit esoteric for most analysis courses.

Paul Halmos was more critical towards Dedekind cuts (Pure Thought Is Better Yet, The College Mathematics Journall, Vol. 16, No. 1 (Jan., 1985), 14-16):

... to define real numbers via Dedekind cuts is bad, and ... As far as Dedekind cuts are concerned, we abstractionists have been arguing against them for a long time; it's not quite honest to dump them in our laps and then accuse us of nurturing them. They are a historical accident. Most students of mathematics learn them as the first logically coherent way of constructing a complete ordered field, but, so far as I know, they are out of fashion by now, or in any event they ought to be. A Dedekind cut is a very narrowly focused concept.

One indication that Halmos may have been mistaken is the astounding development of the surreal numbers by J. Conway which was modeled on Dedekind cuts (On Numbers And Games, A K Peters, 2001).

A most meticulous exposition of Dedekind cuts could be found in Edmund Landau's classic Foundations of Analysis, which builds natural, rational, real and complex numbers starting with Peano axioms. The part covering the cuts and the real numbers takes about one third of the book. However, to give a student a notion of what the cuts are need not take that long. Another classic - A Course in Modern Analysis by E. T. Whittaker and G. N. Watson - introduces the cuts in all of two pages. First published in 1902, it underwent three revision in 1915, 1920, and 1927. The fourth edition became a staple of mathematical libraries and has been reprinted in 1935, 1940, 1946, 1950, 1952, 1958, 1962, 1963, 1996, 1999, 2000, 2002 - all by Cambridge University Press.

Having defined the natural and rational numbers, Whittaker and Watson define the cuts on page 4 and are through with them by page 6. Dedekind cuts (which the authors refer to as partitions or sections) of the set of rational numbers consist of two complementary sets - \(L\)-class and \(R\)-class - that satisfy two conditions:

At least one member of each class exists.
Every member of the \(L\)-class is less than every member of the \(R\)-class.

Any rational number \(x\) defines two such partitions: in one \(x\) is the largest member of the \(L\)-class; in the other it's the smallest member of the \(R\)-class.

There are cuts where neither \(L\)-class has the largest member nor \(R\)-class has the least member. These are identified with the irrational numbers. \(\sqrt{2}\) is used as an example. Let \(L\)-class consist of all rational numbers whose square is less than \(2\), \(R\)-class consists of the remaining rationals. In a footnote on page 5 the authors prove that \(\sqrt{2}\) is irrational (this is proof 8 in our collection). With the reference to the so-defined section the authors say

Then this section is such that the \(R\)-class has no least member and the \(L\)-class has no greatest member; for, if \(x\) be any positive rational fraction and \(\displaystyle y=\frac{x(x^{2}+6)}{3x^{2}+2}\), then \(\displaystyle y-x=\frac{2x(2-x^{2})}{3x^{2}+2}\) and \(\displaystyle y^{2}-2=\frac{(x^{2}-2)^3}{(3x^{2}+2)^2}\), so \(x^2\), \(y^2\) and 2 are in order of magnitude; and therefore given any member \(x\) of the \(L\)-class, we can always find a greater member of the \(L\)-class, or given any member \(x'\) of the \(R\)-class, we can always find a smaller member of the \(R\)-class, such numbers being, for instance, \(y\) and \(y'\), where \(y'\) is the same function of \(x'\) as \(y\) of \(x\).

Since it was shown that \(\sqrt{2}\) is not rational, neither \(L\) nor \(R\) contains an element whose square is \(2\). So that it never happens that \(x = y\), regardless of which of the two classes \(x\) has been picked from, implying that neither has an extremal member.

Having shown that, Whittaker and Watson define operations on cuts. For example, addition of two cuts \((L,R) = (L_{1},R_{1})+(L_{2},R_{2})\) is defined by setting

\(L = \{x+y:\space x \in L_{1}, y\in L_{2}\}\)

with \(R\) containing all the rationals that are not in \(L\). There are things to prove, say, that \(R\) is not empty and that it contains only numbers that are each greater than any member of \(L\); the theory requires a good deal of proving. It is comforting to know that it has been done (see, for example, Edmund Landau's book.) But the idea must be clear. Denote \(\xi=(L,R)\), where \(L=\{x:\space x^2\lt 2\}\). Then, as one would expect, the theory leads to \(\xi ^{2}=2\), making the equations \(x^{2}=2\) solvable with the cuts and giving a reason to denote \(\xi=\sqrt{2}\).

Function \(\displaystyle f(x)=\frac{x(x^{2}+6)}{3x^{2}+2}\) used by Whittaker and Watson is monotone increasing and has \(\sqrt{2}\) as a fixed point. Here is its graph:

a graph of a function from Whittaker and Watson with fixed point at sqrt(2)

Iterations \(x_{k+1}=f(x_{k})\) will stay in \(L\) if started in \(L\), and in \(R\) if started in \(R\). This is not the only function that has this property - not even the simplest one. In a paper published in 1932, two students from OSU suggested a class of simpler functions (Theodore Weaver and Theodore Suckau, A Remark on Dedekind Cuts, Am Math Monthly, Vol. 39, No. 7 (Aug. - Sep., 1932), 413-414). It does not appear that the authors were aware of Whittaker and Watson's classic. They mention that the commonest approach to proving that \(x\) has the requisite property consists in finding for a given rational \(x\in L\) a rational \(h>0\) such that \(x+h\in L\) still; and similarly for the case \(x\in R\). They met this challenge by coming up with the function \(\displaystyle g(x)=\frac{4+3x}{3+2x}\). They wrote

While working on this problem in an introductory course in analysis con- ducted by Professor Tibor Rado at the Ohio State University we found a way of proving this which was both interesting to the class and to the instructor. We thought that it might be interesting to others because of its connection with more advanced mathematics.

Regarding function \(g\), they found that

\(\displaystyle g^{2}(x)=2 + \frac{x^{2}-2}{(3+2x)^{2}}\),

which shows that \(g(x)\) has \(\sqrt{2}\) as a fixed point. Here's a pertinent portion of its graph from which it is clear that the function is also monotone increasing (around \(\sqrt{2}\)):

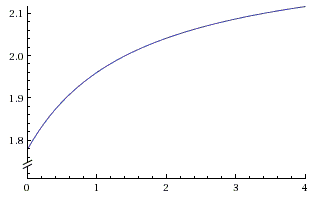
a graph of a function from by two students with fixed point at sqrt(2)

The two Theodores further found that

\(\displaystyle g^{2}(x) - x^{2} = \frac{4(2+3x+x^{2})(2-x^{2})}{(3+2x)^{2}}\),

such that \(g^{2}\) shares the required properties of Whittaker and Watson's \(f\). Additionally, they observed that any function \(\displaystyle g(x)=\frac{bx+2a}{ax+b}\), where \(a\) and \(b\) are positive integers satisfying

\( \bigg| \begin{matrix} b & 2a \\ a & b \end{matrix} \bigg| \space\gt\space 0 \)

would serve faithfully the same purpose.

On the whole, it's a very nice paper from decades (more accurately, epochs) ago. Compared to the classic Whittaker and Watson's text, Weaver and Suckau's paper has one flaw; they never mention the fact that \(\sqrt{2}\) is irrational. As long as that had not been established, the number might belong to \(R\) (since \(L\) has been defined as \(L=\{x:\space x^2\lt 2\}\)); and then the argument falls through.

71537370