Sylvester's Problem, Steinberg's Solution

The Sylvester Problem has been posed by James Joseph Sylvester in 1893 in Educational Times:

Let $n$ given points have the property that the line joining any two of them passes through a third point of the set. Must the $n$ points all lie on one line?

R. Steinberg's was actually the first published solution to Syvester's problem,

Solution

Given the set $\Pi$ of noncollinear points, consider the set of lines $\Sigma$ that pass through at least two points of $\Pi.$ Such lines are said to be connecting. Among the connecting lines, those that pass through exactly two points of $\Pi$ are called ordinary. We consider the configuration in the projective plane.

Let $p$ be any point of $\Pi.$ If $p$ lies on an ordinary line we are done, so we may assume that $p$ lies on no ordinary line. Let $t$ be a line (in the plane) through $p$ but not through any other point of $\Pi.$ The lines in $\Sigma$ not through $p$ meet $t,$ in points $x_{1},x_{2},\ldots,x_{k}$ say, named in cyclic order so that one of the two segments determined by $p$ and $x_1$ contains none of the points $x_{2},\ldots,x_{k}$ within it:

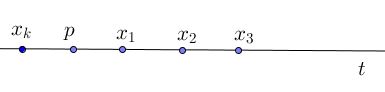
Steinberg's proof of Sylvester's problem, step 1

Let $s$ be a line of $\Sigma$ through $x_1$. Then $s$ must be ordinary!

Steinberg's proof of Sylvester's problem, step 2

For otherwise there would be three or more points of $\Pi$ on $s,$ say $p_{1},p_{2},p_{3}$ named so that $p_1$ and $x_1$ are separated by $p_2$ and $p_3$:

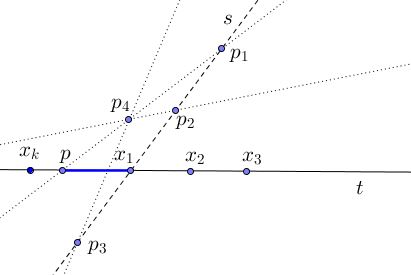
Steinberg's proof of Sylvester's problem, step 3

The connecting line through $p$ and $p_1$ would have to contain a further point of $\Pi$ (remember, $p$ lies on no ordinary line), say $p_4,$ and then one of these two connecting lines $p_{2}p_{4},$ $p_{3}p_{4}$ would meet the "forbidden" segment $px_1.$

References

P. Borwein, W. O. J. Moser, A survey of Sylvester's problem and its generalizations, Aequationes Mathematicae 40 (1990) 111 - 135
H. S. M.Coxeter, A Problem of Collinear Points, The American Mathematical Monthly, Vol. 55, No. 1 (Jan., 1948), pp. 26-28
P. Erdös, R. Steinberg, Problem 4065 [1943, 65]. Proposed by P. Erdös, Princeton, N. J, Solution by Robert Steinberg,S tudent, University of Toronto, The American Mathematical Monthly, Vol. 51, No. 3 (Mar., 1944), pp. 169-171
J. J. Sylvester, Educational Times, Mathematical Question 11851, vol. 59 (1893), p. 98

71947060