Broken Line in Triangle

Let $O$ be a point within $\Delta ABC.$

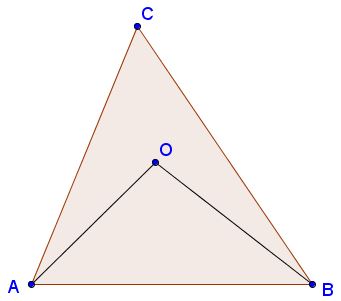
point in triangle - problem

Then $AO+BO\lt AC+BC.$

Proof

Extend $AO$ to intersect $BC$ in $D.$

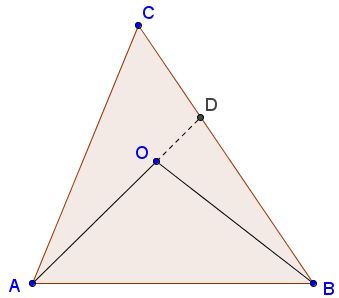
point in triangle - solution

We shall apply the triangle inequality twice:

$\begin{align} \mbox{In}\, \Delta BOD: & BO\le DO+BD,\\ \mbox{in}\, \Delta ACD: & AD\le AC+CD. \end{align}$

Adding the two while replacing $AD$ with $AO+DO$ we obtain

$BO+(AO+DO)\le (DO+BD)+(AC+CD),$

which on reducing $DO$ on both sides and noting that $CD+BD=BC,$ yields

$AO + BO\le AC + BC.$

What remains is to note that there could never be an equality unless $O=C.$ Excluding this possibility, this is always true that $AD\lt AC+CD$ and, when $O\ne D,$ we also have that $AO\lt AD$ so that the resulting inequality is always strict, as required.

Remark 1

The same result could be obtained intuitively by considering the family of confocal ellipses: those with foci at $A$ and $B.$ These ellipses are level curves of the sum of distances from the foci. The level curves never intersect so that one is always within the other.

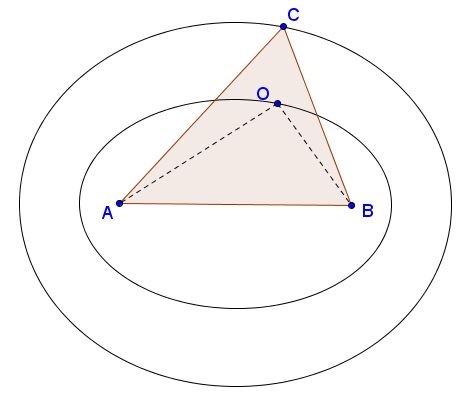
point in triangle - level curves

Remark 2

In fact a more general statement holds: given two polygons - a convex one inside the other (they may share points and segments) - the perimeter of the smaller polygon is smaller than that of the bigger one.

References

S. Dorichenko, A Moscow Math Circle: Week-by-week Problem Sets, MSRI/AMS, 2012, #16.6

71536749