Geometry, Algebra, and Illustrations

A simple multiple choice problem with solution has been posted at the MAA site:

The area of a rectangle ABCD is 72. If point A and the midpoints of BC and CD are joined to form a triangle, the area of the triangle is

triangle cut off rectangle of area 72

The problem came from the 2000 AMC 8 (#25). The solution given is purely algebraic.

Solution

Three triangles lie outside ΔAMN. Their areas are 1/4, 1/4, and 1/8 for a total of 5/8 of the rectangle. The area of ΔAMN is 73·3/8 = 27.

Let the rectangle have sides of 2a and 2b so that 4ab = 72 and ab = 18. Three right triangle lie outside ΔAMN, and their areas are (2a)(b)/2, a(2b)/2, ab/2. for a total of ab·5/2 = 18·5/2 = 45. The area of ΔAMN is 72 - 45 = 27.

Now, the problem is pretty simple, and it was probably the way it was supposed to be solved. However, an illustration would not be amiss:

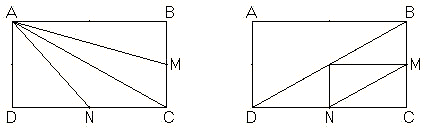
solutions to the problem of a triangle cut off rectangle of area 72

ΔABC whose area is half that of the rectangle is divided into two (ABM and AMC) by the median AM so that each of the smaller triangles has the area 1/4 of that of the rectangle, i.e., 72/4 = 18. Similarly, area(ΔADN) = Area(ΔANC) = 18.

Drawing the second diagonal BD and the midlines of ΔBCD, we see that area(ΔCMN) is 1/8 of that of the rectangle: area(ΔCMN) = 72/8 = 9.

The above solution tells us that

area(ΔAMN) = area(ABCD) - area(ΔABM) - area(ΔADN) - area(ΔCMN) = 72 - 18 - 18 - 9 = 27.

The diagram also suggests another solution:

area(ΔAMN) = area(ΔAMC) + area(ΔANC) - area(ΔCMN) = 18 + 18 - 9 = 27.

While the latter could have been easily derived algebraically, I see the advantage of presenting the diagrammatic solution as less linear and, perhaps, more open minded. One diagram illustrates two solutions at once and serves, if only a little, more educational value than the cited solution.

But is not this the purpose of posting a solution in the first place?!

41170294