An Olympiad Problem With the Floor Function
Problem
Let $n$ be a natural number. Prove that
$\displaystyle\bigg\lfloor\frac{n}{1}\bigg\rfloor +\bigg\lfloor\frac{n}{2}\bigg\rfloor +\bigg\lfloor\frac{n}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{n}{n}\bigg\rfloor + \lfloor\sqrt{n}\rfloor$
is even. ($\lfloor x\rfloor$ is the floor, or the whole part, function.)
Solution 1
The proof is by induction. Denote the expression at hand by $f(n).$ Obviously, $f(1)=2$ and is thus even. Assume $f(k)$ is even. Consider the difference $f(k+1)-f(k).$ The problem will be solved if we show that that difference is always even. But according to a solution to a related problem,
$f(k+1)-f(k)=t_{k+1}+\bigg(\lfloor\sqrt{k+1}\rfloor -\lfloor\sqrt{k}\rfloor\bigg),$
where $t_{k+1}$ is the number of positive divisors $k+1.$ We have
$\lfloor\sqrt{k+1}\rfloor -\lfloor\sqrt{k}\rfloor =\begin{cases} 1,& \mbox{if } k+1 \mbox{ is a square}\\ 0,& \mbox{otherwise}. \end{cases}$
On the other hand $t_{m}$ is odd or even, according to whether $m$ is a square or not. (Usually, the factors come in pairs, like $pq=m.$ But if $pp=m,$ then in the count of factors $p$ has no matching pair.)
It follows that $f(k+1)-f(k)$ is always even, thus completing the inductive step and, with it, the whole proof.
Solution 2
Here we appeal to a geometric configuration similar to one of the proofs of a related problem, where it was found that
$\displaystyle\bigg\lfloor\frac{n}{1}\bigg\rfloor +\bigg\lfloor\frac{n}{2}\bigg\rfloor +\bigg\lfloor\frac{n}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{n}{n}\bigg\rfloor$
is the number of grid points in the first quadrant below and on the hyperbola $y=n/x.$
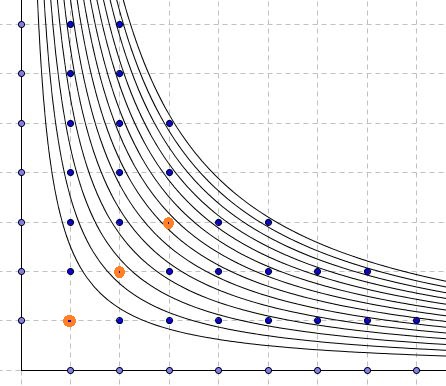
On the other hand, if $p=\lfloor\sqrt{n}\rfloor$ then $p$ is the number of the diagonal points $(q,q)$ below or on the hyperbola. In the expression,
$\displaystyle\bigg\lfloor\frac{n}{1}\bigg\rfloor +\bigg\lfloor\frac{n}{2}\bigg\rfloor +\bigg\lfloor\frac{n}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{n}{n}\bigg\rfloor + \lfloor\sqrt{n}\rfloor$
the diagonal points are counted twice, whereas the number of remaining points is even because $pq\le n$ is symmetric in $p$ and $q$. This shows that the whole expression is even.
Acknowledgment
The problem has been offered at the 29th Indian National Mathematical Olympiad-2014, and the solution #1 is the official one. Solution #2 has been posted by David Angell at the stackexchange.org site. I came across this problem at the Short Mathematical Idea facebook page.
|Contact| |Front page| |Contents| |Algebra| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73579554
