An Equilateral Triangle In Parallel Lines
What Is This About?
Source
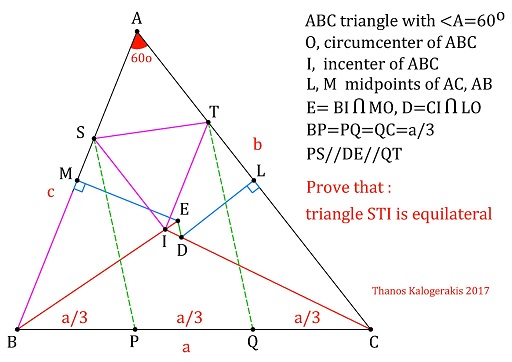
Solution
Note that by the construction triangles $ABE$ and $ACD$ are isosceles. If $\angle ABC=2\beta$ and $\angle ACB=2\gamma$ then $\angle BAE=\beta$ whereas $\angle CAD=\gamma.$ Since $2\beta+2\gamma=120^{\circ},$ $\beta+\gamma=60^{\circ}=\angle BAC,$ the lines $AD$ and $AE$ coincide. In other words, $DE$ passes through $A.$
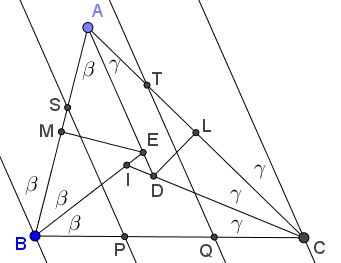
Now, the lines through $B$ and $C$ parallel to $AED$ triple the angles $\beta$ ad $\gamma,$ creating a configuration that was dealt with earlier:
One of the vertices of $\Delta ABC,$ say A, is pushed off to infinity so that the two sides $AB$ and $AC$ and the trisector lines at $A$ become parallel. In this case the angles at $B$ and $C$ are supplementary: $\angle B + \angle C = 180^{\circ}.$ Then the "Morley triangle" is equilateral iff the four lines are equidistant.
Acknowledgment
The problem has been proposed by Thanos Kalogerakis at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group. Thanos then kindly informed me of his post and suggested that the problem was related to a variant of Morley's theorem that was published years ago.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73561852
