Concyclicity in Two Semicircles

This configuration has already been considered elsewhere. The right triangles $ADC,$ $CEB,$ $DCE$ are similar which lays a way of computing the angles $ADE$ and $DEB.$ These can be used to prove that the quadrilateral $ABED$ is cyclic.

Connect $AD,$ $CD,$ $CE,$ $BE.$ Observe that inscribed $\angle CAD$ equals $\angle CDE$ formed in circle $(F)$ by chord $DC$ and the tangent at $D.$ Similarly, $\angle CBE=\angle CED.$

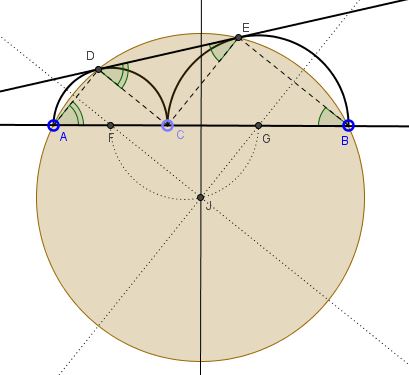
So there are three similar right triangles $ADC,$ $CEB,$DCE.$ Further,

$\begin{align} \angle ADE + \angle ABE &= (90^{\circ}+\angle CDE) + \angle ABE \\ &= 90^{\circ}+(\angle BCE + \angle ABE) \\ &= 90^{\circ}+90^{\circ}=180^{\circ}, \end{align}$

implying that the quadrilateral $ABED$ is indeed cyclic.

In passing, note that the center $J$ of $(ABED)$ lies on the intersection of the perpendicular bisectors of $AB,$ $AD,$ and $BE$ (as these are also chords in $(ABED)$) and the semicircle on $FG$ (because $\Delta FGJ$ is right (and similar to the above mentioned right triangles.)

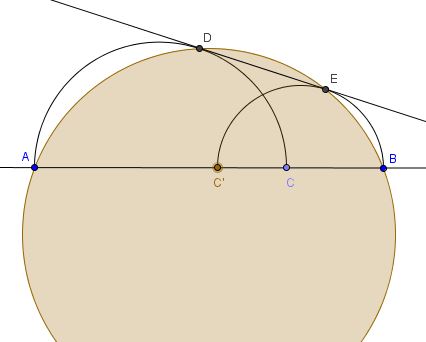
The problem is an auxiliary lemma from a bigger work by Emmanuel Antonio José García. Antonio also observed that the proof never uses the fact that the semicircles are touching. Hence, two additional cases: