Two Regular Pentagons Joined at Vertex

What Is That about?

Problem 1

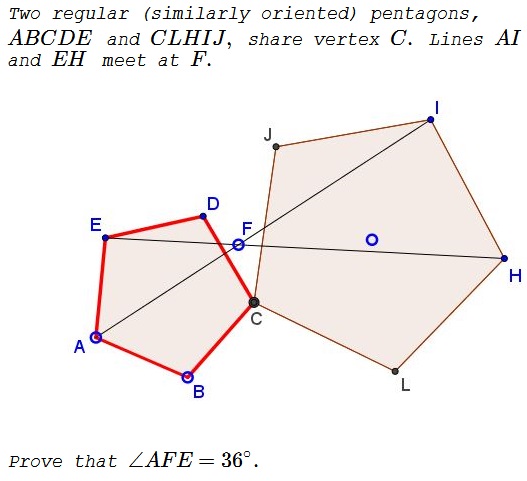
Two Regular Pentagons Joined at Vertex, problem

Problem 2

Two regular (similarly oriented) pentagons, $ABCDE\,$ and $CLHIJ,\,$ share vertex $C.\,$ Lines $AI\,$ and $EH\,$ meet at $F.$

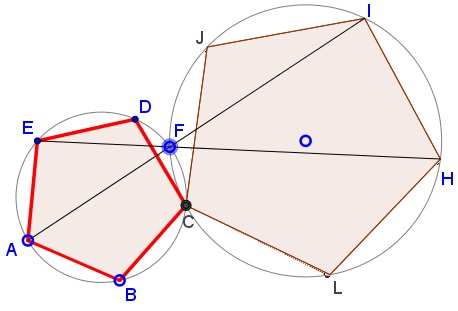
Two Regular Pentagons Joined at Vertex, Illustration 2

Prove that $F\,$ is the second intersection of the circumcircles $(ABCDE)\,$ and $(CLHIJ).$

This can be reformulated as below:

Given a regular pentagon $ABCDE\,$ and point $F\,$ on the arc $\overset{\frown}{CD}\,$ of its circumcircle $(ABCDE).\,$ Circle $(O)\,$ passes through $C\,$ and $F\,$ away from $(ABCDE).\,$ Lines $AF,EF\,$ meet $(O)\,$ the second time at $I\,$ and $H,\,$ respectively.

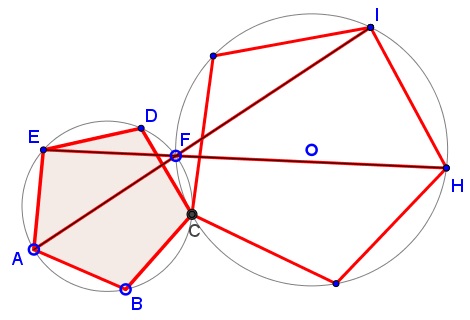
Two Regular Pentagons Joined at Vertex, Illustration 3

Prove that $IH\,$ is a side of a regular pentagon inscribed into $(O),\,$ with $C\,$ one of its vertices.

Solution 1

We'll address the latest reformulation as the most obvious. The crux of the matter is that, regardless of the position of $F\,$ on $\overset{\frown}{CD},\,$ $\angle AFC=72^{\circ}\,$ and $\angle EFC=108^{\circ}\,$ since both are inscribed into $(ABCDE).\,$

Two Regular Pentagons Joined at Vertex, Illustration 4

If so, $\angle CFI=108^{\circ}\,$ and $\angle CFH=72^{\circ},\,$ implying $\angle CIH=72^{\circ},\,$ making $\overset{\frown}{HC}\,$ twice as big as $\overset{\frown}{IH},\,$ which explains the assertion.

Solution 2

Rotation aroun point $C\,$ through $36^{\circ}\,$ sends $\Delta ACI\,$ to $\Delta ECH\,$ and the claim therefore follows.$

Acknowledgement

The problem has been posted on twitter with a GeoGebra illustration by Tim Brzezinski; Steve Phelps join the forces with an illustration of his own; Vincent Pantaloni suggested an explanation. The above is an application of reverse engineering to all of these. Solution 2 is by Dorde Baralic.

72106494