Two Circles, Two Segments - One Ratio
What Is This About?
Problem
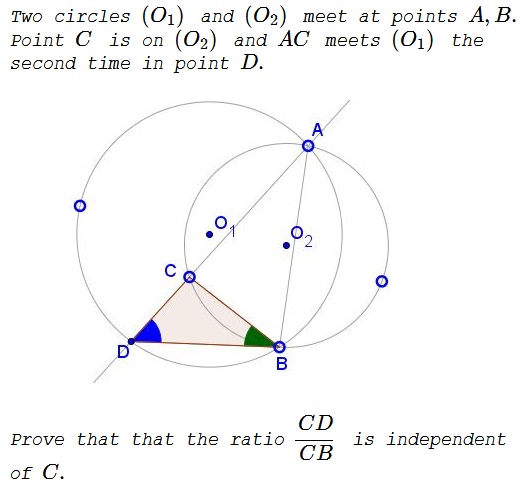
Solution
We have to consider two case, depending on the position of $C:\,$ it may lie either within or without the circle $(O_1).$
Here's the first case:
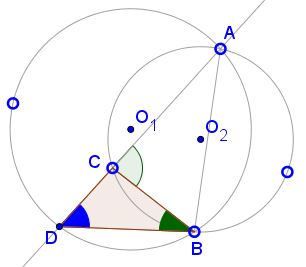
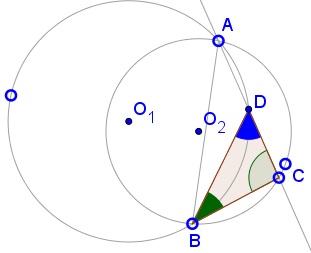
Here's the second case:

In the latter case there is a distinct possibility that point $D\,$ may fall within $(O_2):$
We observe (and plan to prove by pure angle chasing) that the angles in $\Delta BCD\,$ do not depend on the position of $C\,$ on $(O_2).\,$ Due to the Law of Sines, this will settle the claim of the fixed ratio.
In the first case, $\angle BDC=\angle BDA\,$ is inscribed into circle $(O_1)\,$ and is subtend by the arc $\alpha=\overset{\frown}{AB}\,$ which is inside $(O_2).\,$ The same is true in the second case. In the third case, $\angle ADB\,$ supplementary to $\angle BDC,\,$ is subtended by the other arc $\beta=\overset{\frown}{AB}.\,$ Since $\alpha+\beta=360^{\circ},\,$ $\angle BDC\,$ preserves its magnitude in all three cases.
In the last two cases, $\angle BCD=\angle BCA\,$ is inscribed into $(O_2)\,$ and is subtended by the arc $\gamma=\overset{\frown}{AB}\,$ located within $(O_1),\,$ while being an interior angle of $\Delta BCD.\,$ In the first case, it is subtended by the arc $\delta=\overset{\frown}{AB}\,$ outside $(O_1)\,$ while being an exterior angle of $\Delta BCD.\,$ In both case it makes $\angle CBD,\,$ the third angle in $\Delta BCD,\,$ independent of $C.\,$ It follows by the Law of Sines that
$\displaystyle\frac{CD}{CB}=\frac{\sin\angle CBD}{\sin\angle CDB}=\text{const}.$
A special case occurs when $O_1\in (O_2).\,$ This condition lets $C\,$ coincide with $O_1\,$ in which case the triangle $BCD\,$ becomes isosceles, with the ratio of the sides equal to $1.$
Acknowledgment
The problem has been posted on twitter with a GeoGebra illustration by Tim Brzezinski for the particular case when $O_1\in(O_2),\,$ in which case $CD=CB.\,$ Tim credits Antonio Gutierrez from gogeopmetry.com.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73577173
