$(\tan 72^\circ\pm \tan 60^\circ)\sin(30^\circ\mp18^\circ)= 1$
Grégoire Nicollier
University of Applied Sciences of Western Switzerland
April 20, 2017
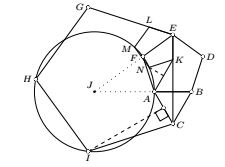
The formula $(\tan 72^\circ + \tan 60^\circ)\sin 12^\circ= 1\,$ proves that the angle in the figure is right (thick equilateral triangle with two thick regular pentagons). The figure also shows the twin construction for $(\tan 72^\circ - \tan 60^\circ)\sin 48^\circ= 1$.
We use $\tan60^\circ=\sqrt3\,$ and $\cos 36^\circ=\varphi/2,\,$ where $\varphi\,$ is the golden ratio. We set $ \tan 72^\circ=t:\,$
$1+t^2 =\sec^2 72^\circ=\bigl(2\cos^2 36^\circ-1\bigr)^{-2}= 4 \varphi^2,$
thus $t^2-3 = 4 \varphi^2 - 4 = 4 \varphi$ and
$\begin{align} \bigl(t\pm\sqrt3\,\bigr)^2 &= \frac{16 \varphi^2}{(t\mp\sqrt3\,)^2}\\ & = \frac{4(1+t^2)}{(t\mp\sqrt3\,)^2} = 1 + \left(\frac{1\pm\sqrt 3t}{t\mp\sqrt3} \right)^2\\ &= 1+ \cot^2(72^\circ\mp60^\circ) \\ &= \csc^2(72^\circ\mp60^\circ)=\csc^2(30^\circ\mp18^\circ). \end{align}$
Thus
$\displaystyle\begin{align} \sin (30^\circ\mp18^\circ)&=\frac1{\sqrt{5+2\sqrt5}\pm\sqrt3}=\frac1{\sqrt{4\varphi^2-1}\pm\sqrt3}\\ &=\frac1{\tan 72^\circ\pm \tan 60^\circ}. \end{align}$
Theorem
The points $H$, $I$, $A$, and $F$ are concyclic.
Proof
We present a proof of K. Knop's statement, different the earlier on. We go the other way round and start from a regular pentagon $HICEG$. Consider the circular arc formed (on the same side of line $HI$ as the pentagon) by the points from where $HI$ subtends an angle of $48^\circ$. Let $J$ be the center of this circle, $F$ the intersection of the circular arc with the perpendicular bisector of $HI$, $A$ the point of the arc on the perpendicular to $CE$ through $J$, and $B$ and $D$ the reflections of $A$ and $F$ across $CE$. Simple angle chasing shows that $IA=IC$, $\angle CEF = 54^\circ$, $\angle EFA = \angle FAB = 108^\circ$, and $\angle BAC = 60^\circ$. We are done if we show that $EF=FA$: then we have a regular pentagon $ABDEF$ and an equilateral triangle $ABC$.
For the proof of $EF=FA$, that is, $\cot18^\circ-\cot24^\circ = 2 \sin18^\circ/\sin48^\circ$, we use the fact that $s=\sin18^\circ$, being equal to $(\varphi - 1)/2$, has the property $2 s^2 = 1/2 - s$. Thus
$\displaystyle \begin{align} \cot18^\circ-\cot24^\circ &= \frac{\sin6^\circ}{s \sin24^\circ}\\ &= \frac{2 \sin6^\circ \cos24^\circ}{s \sin48^\circ}\\ &= \frac{\sin30^\circ-s}{s \sin48^\circ} = \frac{2 s^2}{s \sin48^\circ}. \end{align}$
Theorem
If $K$ is the reflection of $C$ across $AB$ and $KELMN$ the regular pentagon with $L$ on $EG$, $M$ and $N$ lie on the circle of $H$, $I$, $A$, and $F$.
Proof
$EK/EC=(\tan 72^\circ- \tan 60^\circ)/(\tan 72^\circ + \tan 60^\circ) =\sin12^\circ/\sin48^\circ$. If $M'$ and $N'$ are the points of the circle with $\angle M'JF=\angle N'JF=12^\circ$ ($N$ and $N'$ being on the same side of $EJ$), we have thus $M'N'=EK$. But $N'=N$ as $EJ=EC(\cot18^\circ-\cot48^\circ)$ equals $EK(\cot18^\circ+\cot12^\circ)$: this follows from
$\displaystyle \begin{align} \cot18^\circ-\cot48^\circ &=\frac{\sin30^\circ}{\sin18^\circ\sin48^\circ},\\ \quad\cot18^\circ+\cot12^\circ&=\frac{\sin30^\circ}{\sin18^\circ\sin12^\circ}, \end{align}$
and $EC/\sin48^\circ=EK/\sin12^\circ$.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73557789
