K. Knop's Problem with Two Regular Pentagons And an Equilateral Triangle
Problem
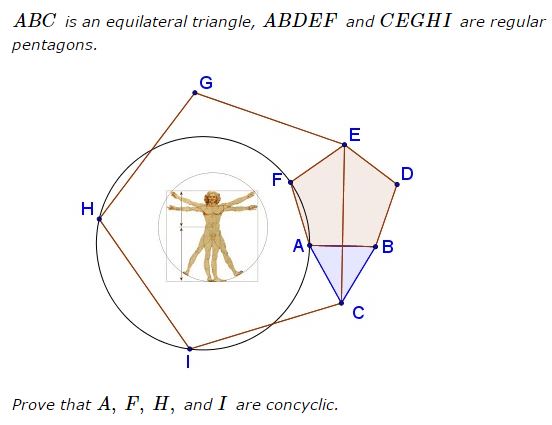
Solution 1
Solution proceeds in several steps. First prove $BI\perp AC\,$ which implies $IA=IC:\,$
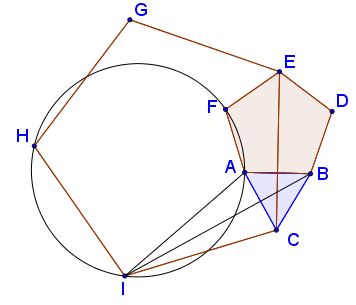
such that
$\angle CAI=\angle ACI=108^{\circ}-30^{\circ}=78^{\circ}.$
Let $J\,$ be the center of the circle $(AHI):$
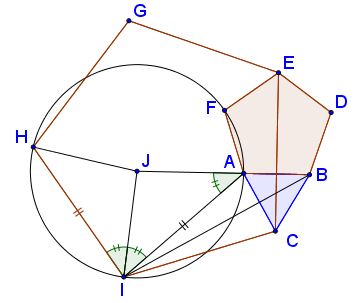
Since $\angle CIA=180^{\circ}-2\cdot 78^{\circ}=24^{\circ},\,$ $\angle AIH=108^{\circ}-24^{\circ}=84^{\circ}.\,$ $IH=IC=IA,\,$ implies $\Delta AIJ=\Delta IJH,\,$ from which $\angle AIJ=\angle JIH=\frac{1}{2}\angle AIH=42^{\circ}.\,$ Further, since $\Delta AIJ\,$ is isosceles, $\angle IAJ=\angle AIJ=42^{\circ}.\,$ By additional angle chasing, $\angle BAI=78^{\circ}+60^{\circ}=138^{\circ},\,$ so that $\angle IAJ+\angle BAJ=180^{\circ}\,$ and $BAJ\,$ is a straight line.
On the other hand, $EF\,$ being the bisector of $\angle CEG,\,$ $EF\perp HI\,$ and passes through the midpoint $K\,$ of the latter.
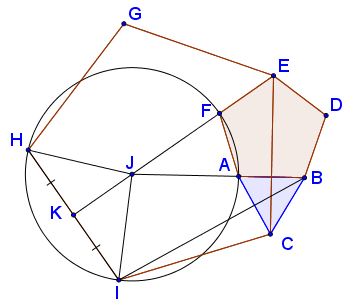
Since the $J\,$ lies on the perpendicular bisector of $HI,\,$ $J\in EK\,$ so that $J\,$ is the intersection of the $AB\,$ and $EF,\,$ extended, which obviously implies that $FJ=AJ,\,$ placing $F\,$ squarely on the circle $(FHI).$
Now, to return to the beginning. The only way I can prove that $BI\perp AC\,$ is by trigonometry.
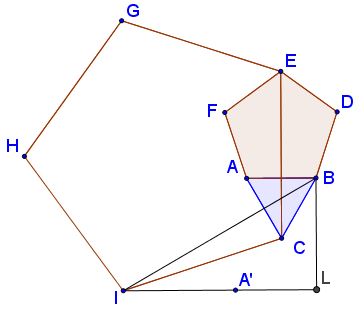
Taking $C\,$ for the origin, with horizontal $x-\text{axis}\,$ and vertical $y-\text{axis}\,$ and assuming $AB=2,\,$ we get $\left(\displaystyle \varphi=\frac{\sqrt{5}+1}{2}\right):$
$\displaystyle \begin{align} &B=(1,\sqrt{3}),\\ &IC=CE=\sqrt{3}+2\cdot\varphi\cdot\cos 18^{\circ}=\sqrt{3}+(\sqrt{5}+1)\frac{\sqrt{2(5+\sqrt{5})}}{4},\\ &\angle CIL=18^{\circ}\,\Rightarrow\,I=IC\cdot(-\cos 18^{\circ},-\sin 18^{\circ}),\\ &\tan\angle BIL=\frac{\sqrt{3}+IC\cdot\sin 18^{\circ}}{1+IC\cdot\cos 18^{\circ}}. \end{align}$
Due to the lack of patience and being sure there ought to be a synthetic shortcut, I ran this ratio by wolframalpha which produced $\displaystyle \frac{1}{\sqrt{3}}\,$ as one of alternative results. Thus, $\tan\angle BIL=\displaystyle \frac{1}{\sqrt{3}},\,$ giving $\angle BIL=30^{\circ},$ as required.
P.S.
Here's a direct proof that $BI\perp AC.\,$ We write $M\,$ for the midpoint of $AC\,$ and $\tan(60^{\circ})=\sqrt{3},\,$ $\tan(72^{\circ})=t\,$ so that $1+t^2 = 4\varphi^2,\,$ and, thus, $t^2-3 = 4 \varphi^2 - 4 = 4\varphi.\,$ Suffice it to show that $\Delta ICM\,$ is right-angled at $M,\,$ that is, that $\csc(12^{\circ}) = t+\sqrt{3}.$
Proof:
$\displaystyle \begin{align} (t+\sqrt{3})^2 &= \left(\frac{4\varphi}{t-\sqrt{3}}\right)^2\\ &= 4\frac{1+t^2}{(t-\sqrt{3})^2}\\ &= 1 + \left(\frac{1+t \sqrt{3}}{t-\sqrt{3}}\right)^2\\ &= 1+ \cot^2(72^{\circ}-60^{\circ})\\ &= \csc^2(12^{\circ}). \end{align}$
Solution 2
Second proof of the problem (the other way round). We start from a regular pentagon $HICEG.\,$ Consider the circular arc formed (on the same side of line $HI\,$ as $E)\,$ by the points from where $HI\,$ subtends an angle of $48^{\circ}.\,$ Let $J\,$ be the center of this circle, $F\,$ the intersection of the circular arc with the perpendicular bisector of $HI,\,$ $A\,$ the point of the arc on the perpendicular to $CE\,$ through $J,\,$ and $B\,$ and $D\,$ the reflections of $A\,$ and $F\,$ across $CE.$

Simple angle chasing shows that $IA=IC,\,$ $\angle CEF = 54^{\circ},\,$ $\angle EFA = \angle FAB = 108^{\circ},\,$ and $\angle BAC = 60^{\circ}.\,$ We are done if we show that $EF=FA:\,$ then we have a regular pentagon $ABDEF\,$ and an equilateral triangle $ABC.$
Proof of $EF=FA,\,$ that is, $\displaystyle \cot(18^{\circ})-\cot(24^{\circ}) = 2\frac{\sin(18^{\circ})}{\sin(48^{\circ})}\,$. We use the fact that $s=\sin(18^{\circ}),\,$ being equal to $\displaystyle \frac{\varphi - 1}{2},\,$ has the property $\displaystyle 2 s^2 = \frac{1}{2} - s.\,$ Thus
$\displaystyle\begin{align} \cot(18^{\circ})-\cot(24^{\circ}) &= \frac{\sin(6^{\circ})}{s\sin(24^{\circ})} = \frac{2\sin(6^{\circ})\cos(24^{\circ})}{s\sin(48^{\circ})}\\ &=\frac{\sin(30^{\circ})-s}{s\sin(48^{\circ})} = \frac{2 s^2}{s\sin(48^{\circ})} = \frac{2 s}{\sin(48^{\circ})}. \end{align}$
and we are done.
Acknowledgment
The problem has been posted at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group by Konstantin Knop.
Konstantin has requested not to leave out a similar problem:
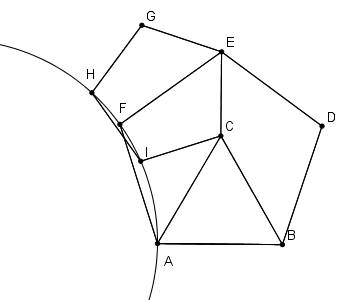
I do leave it as an exercise to the reader. It's the same circle, though.
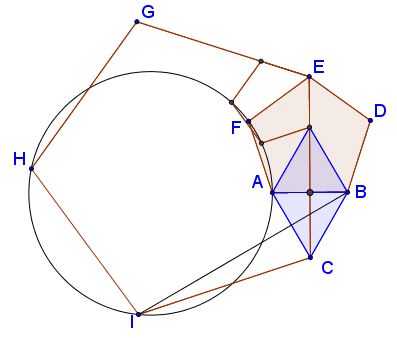
Grégoire Nicollier has come up with a direct proof (P.S.) of $BI\perp AC.$ Konstantin has also added an extra point to the circle on observed that, be symmetry, points C, B, E, O, N are also concyclic.

Grégoire Nicollier has later added another proof (Solution 2), a variant of which has been placed on a separate page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581461
