Construct Triangle by Angle, Median, and Circumradius
What Might This Be About?
Problem
Construct $\Delta ABC,$ given the median $m_b,$ the circumradius $R,$ and the angle $\alpha$ at $A.$
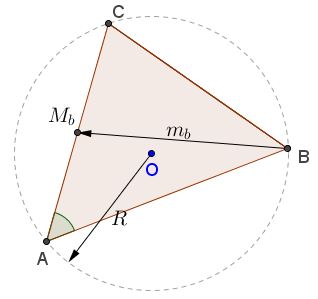
Construction
Note: The construction, as presented, is only valid when $\alpha$ is acute.
Step 1: Construct circle $(O)$ of radius $R$ and a right triangle with hypotenuse on the diameter and one angle $\alpha.$ By the Law of Sines the side of the triangle opposite $\alpha$ will be equal to side $a$ of the sought triangle. We take the end points of that segment as $B$ and $C.$
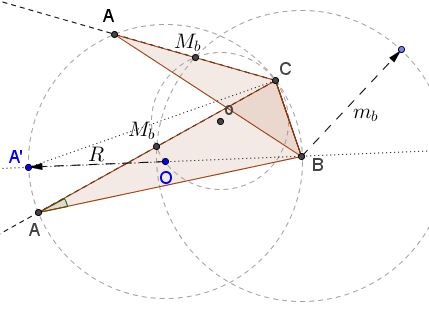
Step 2: Draw circles $C(B,m_b),$ centered at $B$ with radius $m_b,$ and $C(C,R/2)$ centered at $C$ with radius $R/2.$ Their intersections serve as $M_b,$ the foot of the median from $B.$ There could be $0,$ $1,$ or $2$ intersections.
Step 3: Find $A$ at the intersection of $(O)$ and $CM_b.$
Acknowledgment
The construction is due to Prof. Dr. René Sperb.
![]()
|Contact| |Front page| |Contents| |Geometry| |Triangle constructions|
Copyright © 1996-2018 Alexander Bogomolny73578473
