Equilateral triangle and squares
Source
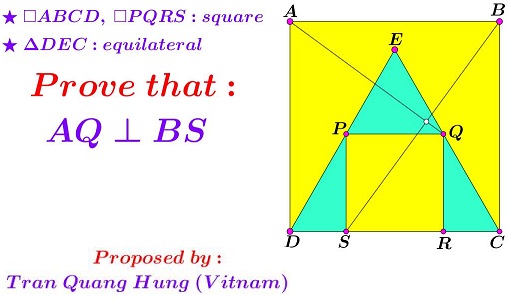
Problem
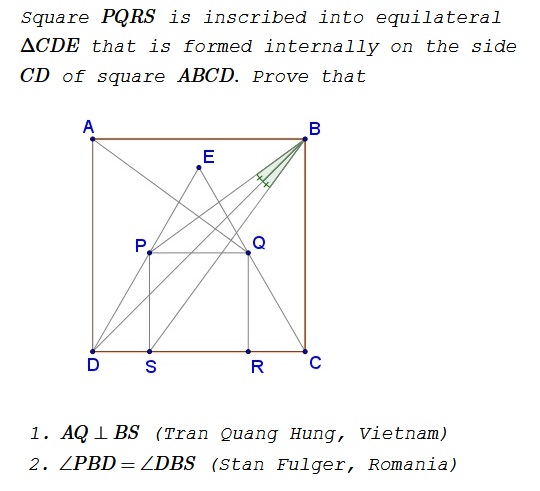
Solution 1
Assume $AB=1$ and denote $SR=x.$ Let $H$ be the intersection of $AD$ and $PQ.$
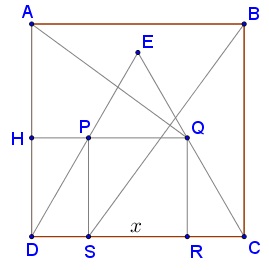
We first show that two right triangles $AHQ$ and $SCB$ are similar. Indeed, in $\Delta DPS,$ the Pythagorean theorem gives $DS^2+PS^2=DP^2,$ i.e., $\displaystyle \left(\frac{1-x}{2}\right)^2+x^2=\left(\frac{2x}{\sqrt{3}}\right)^2$ from which $x=2\sqrt{3})-3.$
To continue, $\displaystyle CS=x+\frac{1-x}{2}=\frac{1+x}{2}$ and similarly $\displaystyle HQ=\frac{1+x}{2}.$ On the other hand, $AH=1-x.$ It is now easy to check that $\displaystyle \frac{AH}{HQ}=\frac{PS}{CS},$ making triangles $AHQ$ and $SCB$ similar. Two pairs of their corresponding sides are perpendicular and so are the remaining pair: $AQ\perp BS.$
Consider $G\in BC$ with $\displaystyle CG=\frac{x}{2}.$ By simple calculations, $G$ is equidistant from $B,$ $P$ and $S.$ Thus, if $GF\parallel CD,$ with $F\in (BPS),$ then $\stackrel{\frown}{PF}=\stackrel{\frown}{FS}.$ Since also $GF=GB,$ $F\in BD,$ proving $\angle PBD=\angle PBF =\angle DBS.$
Solution 2
WLOG, let $AB=1$. Let $SR=p$. Thus, in $\Delta QCR$,
$\displaystyle \tan~60^o=\sqrt{3}=\frac{QR}{RC}=\frac{2p}{1-p}\Rightarrow p=2\sqrt{3}-3.$
Choosing $X$ and $Y$ axes along $BA$ and $BC$,
$\displaystyle \begin{align} \vec{AQ}\cdot\vec{BS}&=\left[\left(\frac{1-p}{2}-1\right)\hat{x}+(1-p)\hat{y}\right]\cdot\left[\left(\frac{1-p}{2}+p\right)\hat{x}+\hat{y}\right] \\ &=\left(-\frac{1+p}{2}\hat{x}+(1-p)\hat{y}\right)\cdot\left(\frac{1+p}{2}\hat{x}+\hat{y}\right)=(1-p)-\frac{(1+p)^2}{4} \\ &=\left(4-2\sqrt{3}\right)-\left(\sqrt{3}-1\right)^2=0. \end{align}$
Thus, $AQ\perp BS$. Let the extension of $BP$ intersect $AD$ at $Z$ and let $\vec{BZ}=\hat{x}+k\hat{y}.$
$\displaystyle \vec{BP}=\left(\frac{1-p}{2}+p\right)\hat{x}+(1-p)\hat{y}=\frac{1+p}{2}\hat{x}+(1-p)\hat{y}.$
Equating the ratios of the $X$ and $Y$ components of $\vec{BP}$ and $\vec{BZ},$
$\displaystyle k=AZ=\frac{2(1-p)}{1+p}=\sqrt{3}-1.$
Also,
$\displaystyle CS=\frac{1-p}{2}+p=\sqrt{3}-1.$
Thus, $AZ=CS$ and by symmetry $\angle ZBD~(=\angle PBD)=\angle DBS$.
Solution 3
We center the coordinates at D. The product of the slopes of AQ and BS is
$\displaystyle \frac{AD-QR}{-RD}\frac{BC}{SC}.$
If we denote $SD=x,SR=y$, the above product is
$\displaystyle \frac{2x(2x+y)}{-(x+y)^2}=-1$
using that $y=\tan(60)=\sqrt{3}x$
- By 1., the rotation counterclockwise at 90 degrees of $BS$ is $AQ$. Also, the rotation at 90 degrees of $BD$ is $AC$. Hence the angle between $BS$ and $BD$ is the one between $AQ$ and $AC$ which is by symmetry same as between $BP$ and $BD$.
Inspiration for 2. D. Schleicher, M.Lackmann, An invitation to mathematics, p.26
Acknowledgment
The problem that was originally posted at the Peru Geometrico facebook group by Miguel Ochoa Sanchez was kindly brought to my attention by Stan Fulger. Solution 2 is by Amit Itagi; Solution 3 is by Bogdan Lataianu.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73575317
