A Problem in Three Pentagons
What Might This Be About?
Problem
Given three regular pentagons - $ACGHI,$ $ABDEF,$ $BCJKL.$
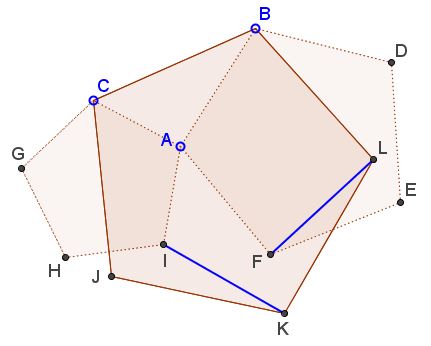
Prove that $FL=IK.$
Solution
Let $M$ be the center of $BCJKL$ and introduce two rotations, $\sigma$ and $\tau:$ $\sigma$ is the counterclockwise rotation around $M$ through $72^{\circ},$ $\tau$ is a counterclockwise rotation around $A$ through $108^{\circ}.$
Obviously, $I=\tau\sigma\tau F.$
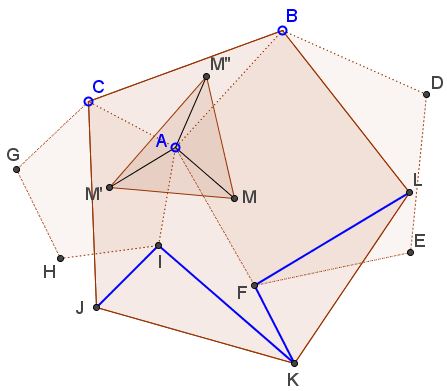
Let $M'=\tau^{-1}M,$ $M''=\sigma^{-1}M',$ $M'''=\tau^{-1}M''.$ From the Lemma below we know that $M'''=M.$ However, $\tau\sigma\tau$ is a rotation by
$108^{\circ}+72^{\circ}+108^{\circ}=288^{\circ}=360^{\circ}-72^{\circ}.$
Since it leaves $M$ in place, this is a rotation by $-72^{\circ}$ around $M$ which is $\sigma^{-1}.$
In other words, $F=\sigma I.$ But observe that also $L=\sigma K$ and $K=\sigma J,$ implying that $\sigma(\Delta IJK)=\Delta FKL,$ making the two triangles equal and rotated $72^{\circ}$ relative to each other.
Lemma
Given an isosceles $\Delta MM'M'',$ with $\angle M'MM''=72^{\circ}.$ Let $A$ be such that $\angle MAM'=\angle M''AM=108^{\circ}.$
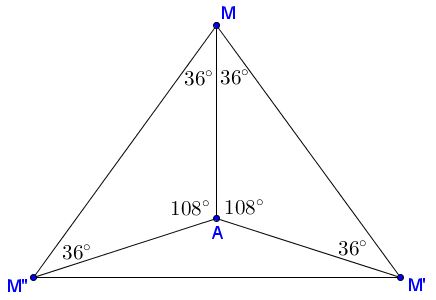
Then $AM=AM'=AM''.$
Acknowledgment
The problem which is due to Ruben Dario from the Peru Geometrico group has been communicated to me by Leo Giugiuc along with his solution in complex numbers.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1966-2016 Alexander Bogomolny73573847
