Thanos Kalogerakis' Collinearity in Triangle
What Is This About?
Source
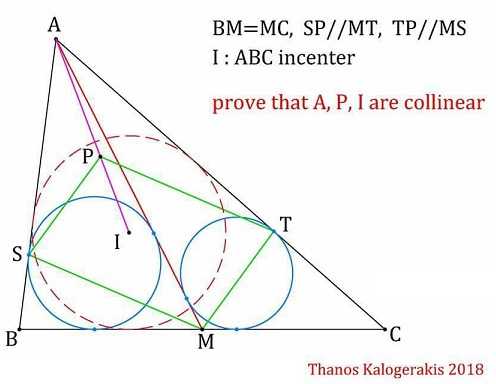
Problem
$M$ is the midpoint of $BC$ in $\Delta ABC;$ $S$ is the intouch point on side $AB$ of $\Delta ABM;$ $T$ is the intouch point on side $AC$ of $\Delta ACM.$ Further, point $P$ inside $\Delta ABC$ satisfies $SP\parallel MT$ and $TP\parallel MS.$
Prove that $A,P,I$ are collinear, where $I$ is the incenter of $\Delta ABC.$
Solution
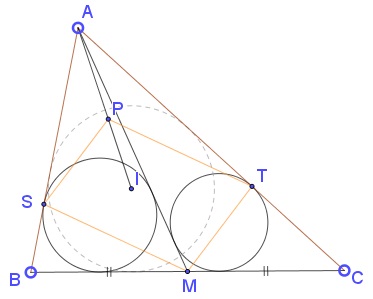
Draw two circle $\displaystyle w_1=C\left(M,\frac{a}{2}\right)$ and $\displaystyle w_2=C\left(A,AM-\frac{a}{2}\right).$ The two circles are tangent to each other at point $Z.$

Let $D$ and $E$ be the point of intersection of $w_2$ with $AB$ and $AC,$ respectively. Then $S$ is the midpoint of $AD$ and $T$ is the midpoint of $BE.$ Indeed, in $\Delta ABM,$ $\displaystyle BS=\frac{1}{2}\left(\frac{a}{2}-AM+c\right)$ whereas $\displaystyle BD=c-\left(AM-\frac{a}{2}\right).$ Similarly, ET=CT.$
By the converse of Varignon's theorem in quadrilateral $BDEC,$ $P$ coincides with the midpoint of $DE$ and, since $\Delta ADE$ is isosceles, $AP$ also serves as the bisector of the angle at $A,$ thus solving the problem.
Acknowledgment
Thanos Kalogerakis has kindly communicated to me his problem along with a solution of his. He also pointed to a post by Reuben Dario at the Peru Geometrico facebook group where one can find additional solutions.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73562218
