Thanos Kalogerakis's Problem in Circle and Square
Source
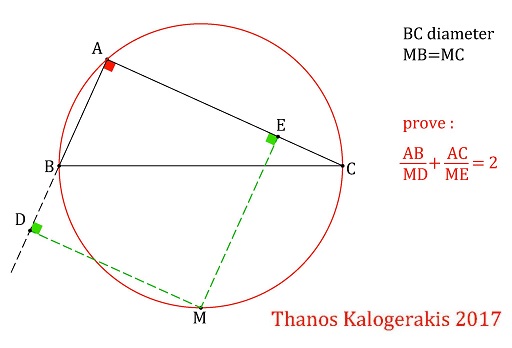
Problem
$BC$ is a diameter of circle $\omega;$ $M$ is the midpoint of one of the arcs $\overset{\frown}{BC};$ point $A$ is on the other arc.
Point $D$ is on line $AB,$ $E$ on line $AC$ such that $MD\perp AB$ and $ME\perp AC.$
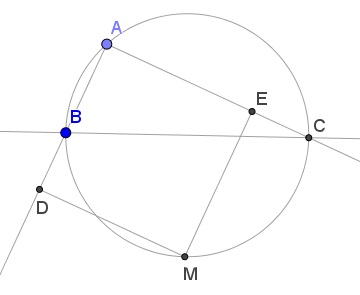
Prove that $\displaystyle \frac{AB}{MD}+\frac{AC}{ME}=2.$
Solution 1
First off, $ADME$ is a square because, due to $M$ being the midpoint of the arc subtending $\angle BAC$ (which is right), $\angle DAM=\angle EAM=45^{\circ}$ and, subsequently, since $ADME$ is clearly a rectangle, $\angle AMD=\angle AME=45^{\circ},$ making $ADME$ a square.
It follows that the required equality can be rewritten as $AB+AC=2MD.$ But, in the diagram, $AC=AE+EC=MD+EC,$ and $AB=AD-BD=MD-BD.$ Adding up gives
$AB+AC=(MD+EC)+(MD-BD)=2MD+(EC-BD).$
Thus the problem will be solved if we show that $EC=BD.$ This is indeed so because triangles $BMD$ and $CM$ are right and equal:
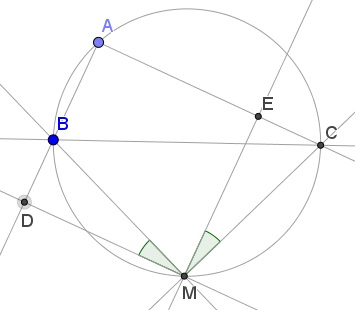
($MD=ME$ and $\angle CME=\angle BMD,$ as having two pairs of perpendicular sides.)
Solution 2
The problem is a particular case of the one discussed earlier:
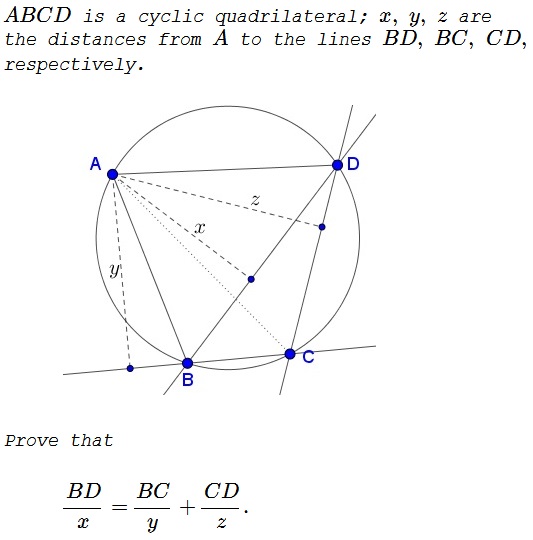
With the reference to the notations in the latter problem, when $BD$ a diameter and $x=R,$ the problem reduces to proving $\displaystyle \frac{BC}{y}+\frac{CD}{z}=2$ which is the original problem in different notations.
Acknowledgment
The problem was posted by Thanos Kalogerakis at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group. Additional solutions can be found at the link.
Solution 2 is by Thanos Kalogerakis.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580675
