An Identity in Cyclic Quadrilateral
Problem
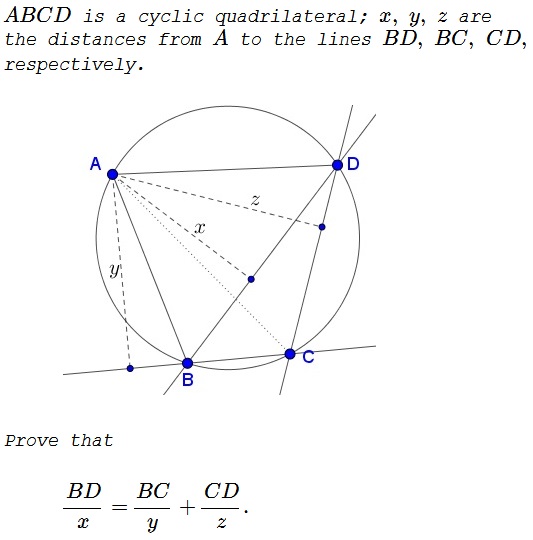
Solution 1
By the Law of Sines, $\displaystyle 2[\Delta ABD]=x\cdot BD=\frac{ad\cdot BD}{2R},$ where $R$ is the circumradius of $\Delta ABC.$ It follows that $\displaystyle x=\frac{ad}{2R}$ and, subsequently, $\displaystyle \frac{BD}{x}=\frac{2R\cdot BD}{ad}.$ Similarly, $\displaystyle \frac{BC}{y}=\frac{2R\cdot b}{a\cdot AC}$ and $\displaystyle \frac{CD}{z}=\frac{2R\cdot c}{d\cdot AC}.$ Thus,
$\displaystyle\begin{align} &\frac{BD}{x}=\frac{BC}{y}+\frac{CD}{z}&\;\Leftrightarrow\\ &\frac{2R\cdot BD}{ad}=\frac{2R\cdot b}{a\cdot AC}+\frac{2R\cdot c}{d\cdot AC}&\;\Leftrightarrow\\ &AC\cdot BD=ac+bd \end{align}$
which is Ptolemey's theorem.
Solution 2
From angles inscribed in the same arcs,
$\angle ADB = \angle ACB$ and $\angle ABD = \angle ACD$.
Thus,
$\displaystyle \begin{align} \frac{x}{y}&=\frac{AD\cdot\sin\angle ADB}{AC\cdot\sin\angle ACB}=\frac{AD}{AC}, \\ \frac{x}{z}&=\frac{AB\cdot\sin\angle ABD}{AC\cdot\sin\angle ACD}=\frac{AB}{AC}. \end{align}$
By Ptolemy's theorem,
$\displaystyle \begin{align} BD &= \frac{AD}{AC}\cdot BC +\frac{AB}{AC}\cdot CD \\ &= \frac{x BC}{y} + \frac{x CD}{z}; \\ \frac{BD}{x}&=\frac{BC}{y}+\frac{CD}{z}. \end{align}$
Acknowledgment
The problem by Deepak Kumar has been kindly communicated to me by Leo Giugiuc, along with a solution of his (Solution 1). Solution 2 is by Amit Itagi. The problem has been originally posted at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518443
