Emil Stoyanov's From Reflections to Altitudes
Problem
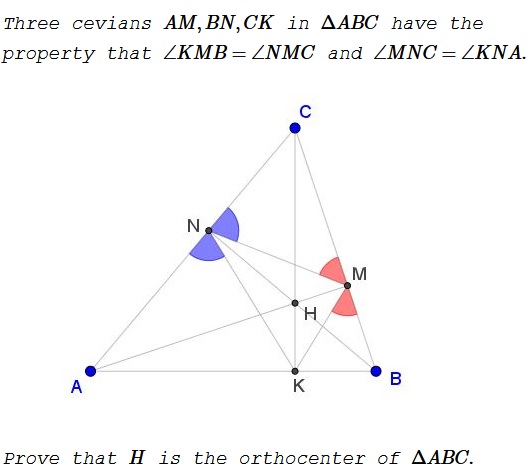
Solution 1
If $\Delta ABC$ is not acute, the problem is meaningless. Let $\alpha=\angle KMB=\angle NMC$ and $\beta=\angle MNC=\angle KNA.$ Also, denote $S=[\Delta ABC];$ $\displaystyle \frac{MB}{MC}=\frac{z}{y},$ $\displaystyle \frac{NC}{NA}=\frac{x}{z},$ $\displaystyle \frac{KA}{KB}=\frac{y}{x},$ where $x,y,z\gt 0.$ (This is possible by Ceva's theorem.) Clearly,
$\displaystyle\begin{align} &[\Delta ANK]=\frac{yz}{(x+y)(z+x)}\cdot S,\\ &[\Delta BKM]=\frac{zx}{(x+y)(y+z)}\cdot S,\\ &[\Delta CMN]=\frac{xy}{(y+z)(z+x)}\cdot S.\end{align}$
However, say,
$\displaystyle [\Delta BKM]=\frac{MB\cdot MK\cdot\sin\alpha}{2}=\frac{az\cdot MK\cdot\sin\alpha}{2(y+z)},\,$ implying $\displaystyle \frac{az\cdot MK\cdot\sin\alpha}{2(y+z)}=\frac{xz}{(x+y)(y+z)}\cdot S,$ so that $\displaystyle \sin\alpha=\frac{2xS}{a\cdot MK(y+y)}.$ Similarly (from $\Delta CMN),$ $\displaystyle \sin\alpha=\frac{2xS}{a\cdot MN(x+z)},$ and we deduce that $\displaystyle \frac{MN}{MK}=\frac{x+y}{x+z}.$ By analogy, from triangles $CMN$ and $ANK,$ $\displaystyle \frac{MN}{NK}=\frac{x+y}{y+z}.$
Thus $\displaystyle \frac{MK}{NK}=\frac{x+z}{y+z}.$ Using the converse way from the above, we obtain $\sin\angle BKM=\sin\angle AKN.$ So the angles $BKM$ and $AKN$ are either equal or supplementary. The latter is impossible, hence they two are equal. Let $\gamma=\angle BKM=\angle AKN.$ We have
$\left\{\begin{align} \alpha+\beta &= \pi-C\\ \beta+\gamma &= \pi-A\\ \gamma+\alpha &= \pi-B \end{align}\right.$
from which $\alpha =A,$ $\beta=B,$ $\gamma=\pi-C,$ implying that the lines $KN,KM,MN$ are antiparallel to the corresponding side lines of $\Delta ABC.$ Further, the angles of $\Delta MNK$ are $\pi-2A,$ $\pi-2B,$ $\pi-2C$ which makes $\Delta KMN$ similar to the orthic $\Delta XYZ$ and their corresponding sides parallel. If the two are not congruent, so that, e.g., $M\ne X,$ then either $MK\lt XZ$ and $MN\gt XY$ or $MK\gt XZ$ and $MN\lt XY.$ In both cases, the triangles $MNK$ and $XYZ$ cannot be similar. Thus $M=X$ and, similarly, $N=Y$ and $K=Z$ which completes the proof.
Solution 2
Let $\angle CNM=\angle ANK=x;$ $\angle CMN=\angle BMK=y.$ By the Law of Sines,
$\displaystyle \begin{align} \text{In }\Delta CMN, & \qquad\frac{CN}{CM}=\frac{\sin y}{\sin x} && (1)\\\\ \text{In }\Delta ANK, & \qquad\frac{AN}{AK}=\frac{\sin \angle NKA}{\sin x} && (2)\\\\ \text{In }\Delta BMK, & \qquad\frac{BK}{BM}=\frac{\sin y}{\sin \angle MKB} && (3) \end{align}$
By Ceva's theorem in $\Delta ABC,$
$\displaystyle \begin{align} \frac{AK}{BK}\cdot\frac{BM}{CM}\cdot\frac{CN}{AN}&=1\\ &=\frac{AK}{AN}\cdot\frac{BM}{BK}\cdot\frac{CN}{CM}\\ &=\frac{\sin x}{\sin\angle NKA}\cdot\frac{\sin\angle MKB}{\sin y}\cdot\frac{\sin x}{\sin y}\\ &=\frac{\sin\angle MKB}{\sin\angle NKA}=1. \end{align}$
It follows that $\sin\angle MKB=\sin\angle NKA.$ Since $\angle MKB +\angle NKA\lt 180^{\circ},$ we deduce $\angle MKB=\angle NKA=z.$
$\displaystyle \begin{align} \text{In }\Delta CMN, & \qquad x+y=180^{\circ}-C=A+B\\\\ \text{In }\Delta ANK, & \qquad x+z=180^{\circ}-A=B+C\\\\ \text{In }\Delta BMK, & \qquad y+z=180^{\circ}-B=A+C. \end{align}$
Solving the system, we obtain $x=B,$ $y=A,$ $z=C.$ Further, $NM$ is antiparallel to $AB,$ making the quadrilateral $ANMB$ cyclic; and so are the quadrilaterals $BKNC$ and $CMKA.$
$\displaystyle \begin{align} \text{Since the quadrilateral }ANMB\text{ is cyclic, } & \angle ANB=\angle BMA=\alpha\\\\ \text{Since the quadrilateral }BKNC\text{ is cyclic, } & \angle BKC=\angle CNB=\beta\\\\ \text{Since the quadrilateral }CMKA\text{ is cyclic, } & \angle CMA=\angle AKC=\gamma. \end{align}$
However, $\angle ANB+\angle CNB=180^{\circ}=\alpha+\beta,$ $\angle AKC+\angle BKC=180^{\circ}=\gamma+\beta,$ $\angle BMA+\angle CMA=180^{\circ}=\alpha+\gamma,$ implying $a=b=c=90^{\circ},$ i.e., $AM,BN,CK$ are the altitudes and $H$ the orthocenter of $\Delta ABC.$
Acknowledgment
This remarkable problem was kindly posted at the CutTheKnotMath facebook page by Emil Stoyanov. Solution 1 is by Leo Giugiuc; Solution 2 is by Marian Dinca.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581271
