Emil Stoyanov's New Year's Problem
What Is This About?
Source
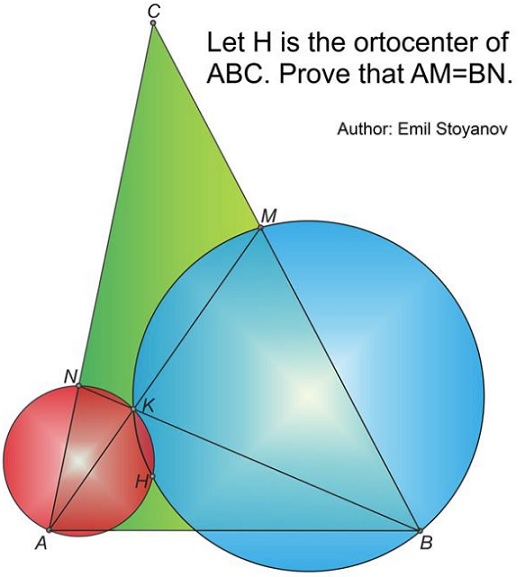
Problem
In $\Delta ABC,\,$ $M\in BC,\,$ $N\in AC;\,$ $K=AM\cap BN;\,$ the circumcircles $(AKN)\,$ and $(BKM)$ intersect a the orthocenter $H\,$ of $\Delta ABC.$
Prove $AM=BN.$
Solution 1
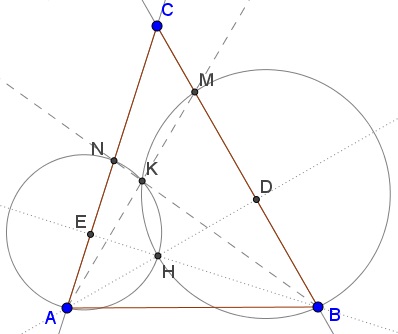
Let $AD\,$ and $BE\,$ be two altitudes in $\Delta ABC.\,$ Since $\Delta BEC\,$ is right, $\angle MBH=\angle CBE=90^{\circ}-\angle C.\,$ Similarly, $NAH =90^{\circ}-\angle C.\,$
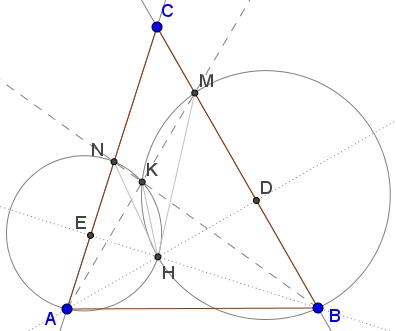
As two inscribed angles subtended by the same arc, $\angle BMH=\angle BKH,\,$ so that $\angle HKN =180^{\circ}-\angle BMH.\,$ But also $\angle HKN =180^{\circ}-\angle NAH,\,$ implying $\angle BMH = \angle NAH = \angle 90^{\circ}-\angle C =\angle MBH.\,$ This makes $\Delta BHM\,$ isosceles, implying that the same is true for $\Delta BAM:\,\,$ $AM=AB.\,$ Similarly we show that $BN=AB\,$ and, therefore, $AM=BN.$
Solution 2
We'll assume, as in the diagram, that $\Delta ABC\,$ is acute. Let $D\,$ and $E\,$ be the projections of $A\,$ and $B\,$ on $BC\,$ and $AC,\,$ respectively. We'll work in complex numbers. Since $BHKM\,$ is cyclic, $\displaystyle\frac{K-M}{B-M}\cdot\frac{B-H}{K-H}\lt 0.\,$ From the diagram, $K-M=\alpha (A-K),\,$ $B-M=\beta (B-C),\,$ with $\alpha, \beta \gt 0.\,$ Thus, $\displaystyle\frac{A-K}{B-C}\cdot\frac{B-H}{K-H}\lt 0.\,$ Similarly, $\displaystyle\frac{B-K}{A-C}\cdot\frac{A-H}{K-H}\lt 0.\,$ Dividing one by another gives
$\displaystyle\frac{A-K}{B-K}\cdot\frac{A-C}{B-C}\cdot\frac{B-H}{A-H}\gt 0.\,$
Now, we have three positively oriented triangles, with the following implications:
$\displaystyle\begin{align} \Delta KAB:\; & \frac{A-K}{B-K}=\frac{AK}{BK}e^{-i\angle AKB}\\ \Delta CAB:\; & \frac{A-C}{B-C}=\frac{AK}{BK}e^{-i\angle C}\\ \Delta HAB:\; & \frac{B-H}{A-H}=\frac{AK}{BK}e^{i(\angle B+\angle C)}. \end{align}$
We deduce that
$\displaystyle\begin{align} 0&\lt \frac{A-K}{B-K}\cdot\frac{A-C}{B-C}\cdot\frac{B-H}{A-H}\\ &=\frac{AK}{BK}\cdot\frac{AC}{BC}\cdot\frac{BH}{AH}e^{i(-\angle AKB-\angle C+\angle A+\angle B)} \end{align}$
From which it follows that $\angle AKB=-\angle C+\angle A+\angle B\,$ and, subsequently, $\angle MKB=2\angle C.\,$ As two inscribed angles, $\angle MHB=\angle MKB=2\angle C.\,$ Finally, since $\angle MBH=90^{\circ}-\angle C,\,$ $\Delta MHB\,$ is isosceles and so is $\Delta MAB,\,$ making $AM=AB.\,$ Similarly, $BN=AB.\;$ By transitivity, $AM=BN.$
Extras
Extra 1 (Statement: Leo Giugiuc; proof: Leo Giugiuc)
$KH\,$ is the internal bisector of $\angle AKB.$
Indeed, $\angle BKH=\angle BMH=\angle MBH=90^{\circ}-\angle C.\,$ Similarly, $\angle AKH=90^{\circ}-\angle C.$
Extra 2 (Statement: Leo Giugiuc; proof: Leo Giugiuc)
Let $P\,$ and $Q\,$ be the second intersections of $(AKH)\,$ and $(BKH),\,$ respectively, with $AB.\,$ Then $AQ=AK\,$ and $BP=BK.$
By Power of a Point theorem, $AK\cdot AM=AQ\cdot AB,\,$ and since $AM=AB,\,$ then $AQ=AK.\,$ $BP=BK\,$ is shown similarly.
Extra 3 (Statement: Sorin Borodi; proof: Leo Giugiuc)
$CP=CQ.$

Indeed, $\angle HPQ=\angle AKH\,$ and $\angle HQP=\angle BKH\,$ and, since $\angle AKH=\angle BKH,\,$ also $\angle HPQ=\angle HQP.\,$ So that, in $\Delta HPQ,\,$ the altitude from $H\,$ is also the median, making $CH\,$ both the alitude and the median from $C\,$ in $\Delta CPQ\,$ such that the triangle is isosceles: $AP=CQ.$
Extra 4
Let $U\,$ be the second intersection of $BE\,$ with $(AKN),\,$ $V\,$ the second intersection of $AD\,$ with $(BKM).\,$
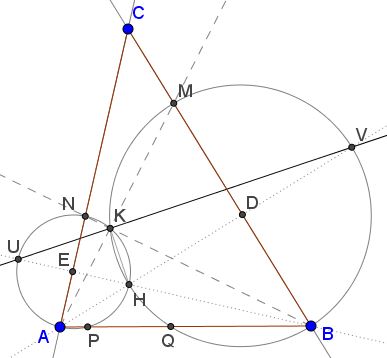
Then $UH\,$ is a diameter of $(AKN),\,$ $VH\,$ is a diameter of $(BKM).$
Suffice it to observe that, say, $E\,$ is the midpoint of $AN\,$ and $BE\perp AN.\,$ Since the perpendicular from the center of a circle bisects a chord, $UH\,$ is bound to pass through the center of $(AKN),\,$ which makes it a diameter.
As a consequence, $\angle HKU=90^{\circ}.\,$ Similarly, $\angle HKV=90^{\circ}.\,$ Thus, in particular, $U,K,V\,$ are collinear and $UV\,$ serves as the external bisector of $\angle AKB.$ In particular, $UV\,$ bisects $\angle BKM\,$ and $\angle AKN.$
Extra 5
Let $T\,$ be the second intersection of $UV\,$ with $(AKB).\,$
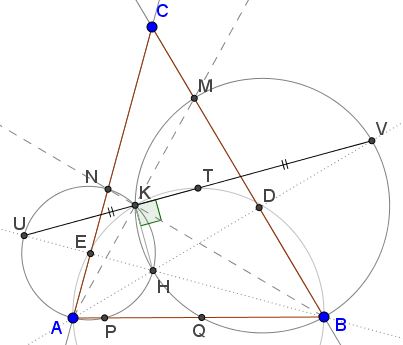
Then $T\,$ is the midpoint of $UV.$
Extra 6 (Statement: Emil Stoyanov)
Let $T\,$ be the second intersection of $(KMN)\,$ and $(ABK).\,$ Then $\angle HKT=90^{\circ}.$
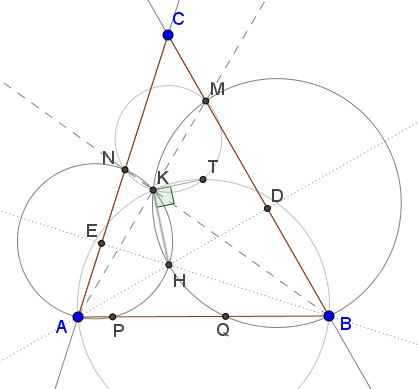
In particular, point $T\,$ coincides with point $T\,$ from Extra 5.
Extra 7 (Statement: Emil Stoyanov)
The center $O_1\,$ of $(AKN)\,$ and the center $O_2\,$ of $(BKM)\,$ lie on $(AKB).\,$ Obviously $H\,$ serves the incenter of $\Delta AKB.$

Extra 8 (Statement: Emil Stoyanov)
The point $T\,$ from Extra 6 has additional related properties:
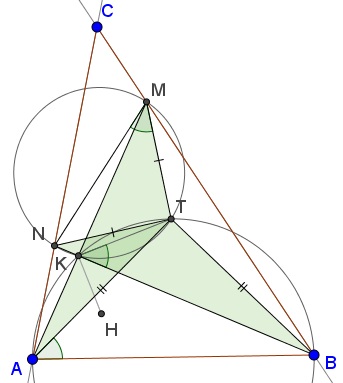
- $AT=BT,\,$ $NT=MT.$
- $\Delta AMT\sim\Delta BNT,\,$ and, in fact, $\Delta AMT=\Delta BNT.$
- $KT\,$ is the external angle bisector of $\angle AKB.$
Acknowledgment
The problem above has been kindly posted by Emil Stoyanov at the CutTheKnotMath facebook page, with New Year greetings. Solution 1 has been arrived at in online collaboration with Leo Giugiuc who also came up with a partially analytic solution (Solution 2). Leo Giugiuc, Sorin, Borodi, and Emil Stoyanov have discovered additional properties of the configuration. These are collected in the Extra part, with authorship assigned per item. This part of the page grew up to such an extent that when more features have been discoeverd by a Romanian teacher Gabriela Negutescu, I decided to put them on a separate page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578707
