Six Concyclic Points via Antipedal Triangle
What Might This Be About?
Problem
$D$ a point in the plane of (non-degenerate) $\Delta ABC.$ Lines $d_a,$ $d_b,$ $d_c$ through $A,$ $B,$ and $C,$ are perpendicular to $AD,$ $BD,$ $CD,$ respectively. $A_1$ is the intersection of $d_b$ and $d_c;$ $B_1$ the intersection of $d_b$ and $d_c;$ $C_1$ that of $d_a$ and $d_b.$ Circles $(A_1),$ $(B_1),$ $(C_1),$ centered at $A_1,$ $B_1,$ $C_1$ and passing through $D,$ meet the side lines of $\Delta ABC$ in six points $A_b,$ $A_c,$ $B_a,$ $B_c,$ $C_a,$ $C_b,$ as shown below.
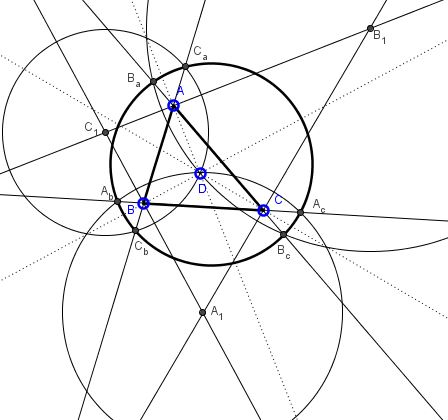
Prove that the six points are concyclic.
In passing, $\Delta A_{1}B_{1}C_{1}$ is known as the antipedal triangle of point $D$ with respect to $\Delta ABC.$
Solution
Circles $(B_1)$ and $(C_1)$ intersect in $D$ and one other point, say $A'$ - its mirror image in the line of centers $B_{1}C_{1},$ or point $A,$ which is the same:
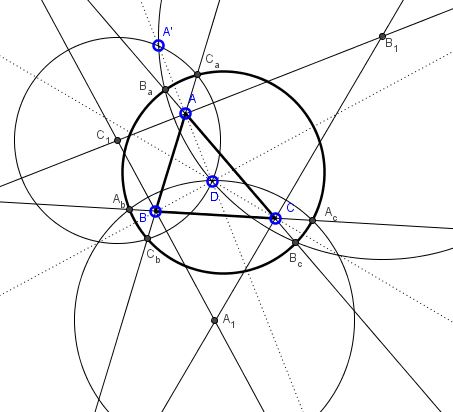
According to the Power of a Point Theorem, in circle $(B_1),$ $AB_a\times AB_c=AD\times AA' = AD^2.$
On the other hand, in circle $(C_1),$ $AC_a\times AC_b=AD\times AA' = AD^2,$ implying, by the the inverse of the Power of a Point Theorem, that points $B_a,$ $B_c,$ $C_a,$ $C_b$ are concyclic. Similarly, points $C_a,$ $C_b,$ $A_b,$ $A_c,$ are concyclic, and so are points $A_b,$ $A_c,$ $B_a,$ $B_c.$ Assuming the circles are distinct, the side lines of $\Delta ABC$ serve as radical axes of the pairs of the circles. This leads to a contradiction because the triangle is non-degenerate, whereas the three radical axes of three circles taken in pairs meet at their radical center. It follows that the three circles coincide, making all six points concyclic.
Acknowledgment
The problem and its solution have been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579071
