Kiepert's Triangles Graduate to Ears of Arbitrary Shape
What is this about?
Problem
On the side of $\Delta ABC$ construct similarly oriented similar triangles $ABN_{c},$ $BCN_a,$ and $CAN_b.$
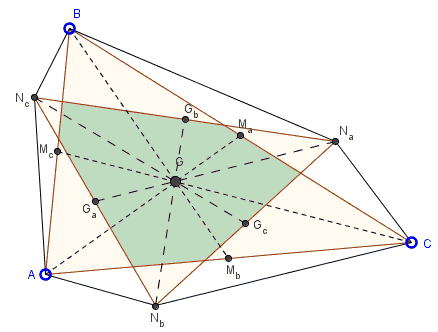
Prove that the centroids of triangles $ABC$ and $N_{a}N_{b}N_{c}$ coincide.
Hint
I think in complex numbers the proof is exceptionally simple. In affine geometry, though, it is no more difficult.
Solution
Let in a complex plain, the vertices of $\Delta ABC$ correspond to complex numbers $\alpha,$ $\beta,$ $\gamma.$

Then, if $i^{2}=-1$,
$N_{a}=\gamma + t(\beta -\gamma),$
$N_{b}=\alpha + t(\gamma -\alpha),$
$N_{c}=\beta + t(\alpha -\beta),$
for some complex $t$ that determines a base angle and the corresponding side length of the formed triangles.
The centroid of $\Delta ABC$ is given by $(\alpha +\beta +\gamma)/3$ while that of $\Delta N_{a}N_{b}N_{c}$ is
$\displaystyle \begin{align} \frac{[\gamma + t(\beta -\gamma)] + [\alpha + t(\gamma -\alpha)] + [\beta + t(\alpha -\beta)]}{3} \\ &= \frac{\alpha +\beta +\gamma}{3}. \end{align} $
Acknowledgment
I am sincerely grateful to Grégoire Nicollier who has kindly pointed out that the statement proved for Kiepert's isosceles triangles has an immediate extension to similar triangles of arbitrary shape, as above.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581320
