Seven Equal Circles
What is this about?
Problem
In $\Delta ABC,$ $A',B',C'$ are the feet of altitudes to the sides $BC,$ $AC,$ and $AB,$ while $A{''},B^{\space}{''},C^{\space}{''}$ are the midpoints of those sides; $H$ is the orthocenter, $H_{a}, H_{b},H_{c}$ are the midpoints of $AH,$ $BH,$ and $CH,$ respectively.

Prove that the circumcircles of triangles $AB^{\space}{''}H_{a},$ $CB^{\space}{''}H_{c},$ $CA{''}H_{c},$ $BA{''}H_{b},$ $BC^{\space}{''}H_{b},$ $AC^{\space}{''}H_{a},$ and $A{''}B^{\space}{''}C^{\space}{''}$ are all equal.
Hint
Observe that circumcircle $(A{''}B^{\space}{''}C^{\space}{''})$ is the famous nine-point circle which is known to have the radius which is exactly half of the circumradius of $\Delta ABC.$ Also, recollect that the vertices, the orthocenter, the sides, and the altitudes of a triangle are all a part of a remarkable configuration, with unusual properties.
Solution
The first six circles are homothetic to one of the three circles through two vertices and the orthocenter of $\Delta ABC,$ with one of the vertices as the center and $2$ as the coefficient of homothety.
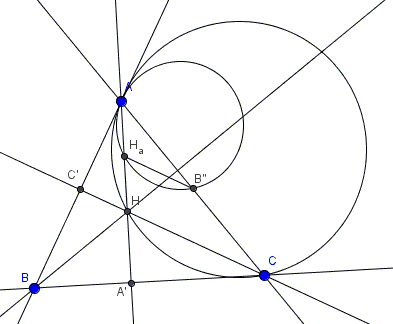
The circumcircles of triangles $ABH,$ $BCH,$ $ACH,$ and $A'B'C'$ are known to be equal, while the latter - the nine-point or Euler's circle - also passes through points $A{''},B^{\space}{''},C^{\space}{''}$ and $H_{a},H_{b},H_{c}.$
Additionally, the nine-point circle is known to have the radius which is exactly half of the circumradius of $\Delta ABC.$
Acknowledgment
This problem has been posted at the CutTheKnotMath facebook page by Dao Thanh Oai.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580867
