One More Seven Circles Theorem
What Might This Be About?
Problem
Let circle (1) touch circle (2) at $A_3$ and circle (3) touch circle (4) at $B_3$. Let circle (1),(2),(3),(4) touch circle $(O)$ at $A_1,A_2,B_1,B_2.$ Let $O_a$ be the center of $(A_1A_2A_3),$ $O_b$ the center of $(B_1B_2B_3).$
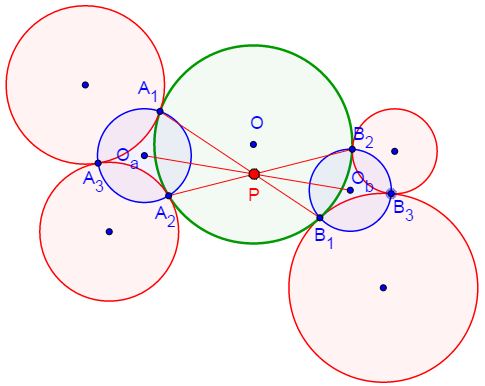
Show that $A_1B_1,$ $A_2B_2$ and $O_aO_b$ are concurrent.
Proof 1
Let $X=A_1A_2 \cap B_1B_2,\;Y=A_1B_2 \cap A_2B_1$.
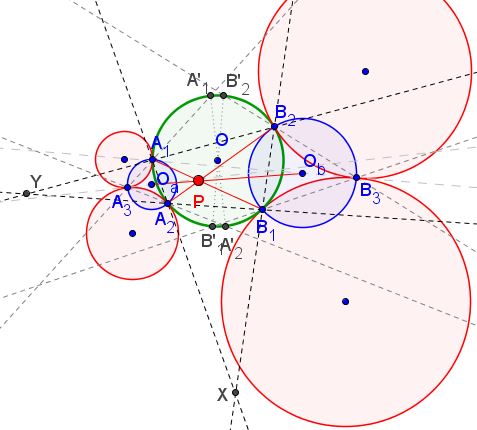
Let $\ell_A, \ell_B$ be the common tangent of circles (1), (2) and (3),( 4), respectively. Let $A_3A_1, A_3A_2, B_3B_1, B_3B_2$ cut $(O)$ again at $A_1^', A_2^', B_1^', B_2^'$, respectively.
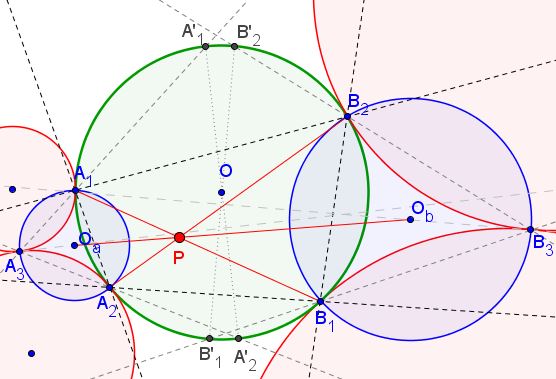
The homothety with center $A_1$ that maps circle (1) to $(O)$ maps the tangent of circle (1) at $A_3$ to the tangent to $(O)$ at $A'_1,$ making the later parallel to $\ell_A$. Similarly, we can get the tangent to $(O)$ through $A'_2$ is parallel to $\ell_A,$ implying that $A'_1A'_2$ is the diameter of $(O)$.
From $\angle OA_1A_2=\angle OA_2A_1=90^{\circ}-\angle A_2A_3A_1$ it follows that $O_aA_1$ and $O_aA_2$ are the tangents of $(O)$. Similarly, $O_bB_1$ and $O_bB_2$ are also tangent to $(O).$ Thus, $O_aO_b$ is the polar of $A_1A_2 \cap B_1B_2 \equiv X$ with respect to $(O),$ so we conclude that $A_1B_1,$ $A_2B_2,$ $O_aO_b$ are concurrent at the pole of $XY$ with respect to $(O)$.
Q.E.D
Proof 2
If $(O_1),(O_2)$ denote the circles (1),(2), then clearly $(O_a)$ is the incircle of $\triangle OO_1O_2,$ implying that $(O_a)$ is orthogonal to $(O)$ and similarly $(O_b)$ is orthogonal to $(O).$ Inversion with center $P$ and power $PA_1 \cdot PB_1=PA_2 \cdot PB_2$ fixes $(O)$ and swaps $(O_a),(O_b)$ due to conformity. Hence, $O_a$ and $O_b$ are collinear with the center of the inversion $P.$
Acknowledgment
The above theorem is by Dao Thanh Oai (Vietnam) who posted at the CutTheKnotMath facebook page the theorem itself, a link to a GeoGebra applet, and a proof by Telv Cohl.
Dao Thanh Oai has also observed that using Brianchon's theorem the above implies the original Seven Circles Theorem. The secnd proof is by Luis González
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581266
