Yet Another Seven Circles Theorem

What Might This Be About?

Problem

Let $P$ be a point in the plane of $\Delta ABC.$ $AP,$ $BP,$ $CP$ meet the circumcircle $(O)$ of $\Delta ABC$ again at $A_1,$ $B_1,$ $C_1,$ respectively. Define $A_b$ and $A_c$ as the circumcenters of $\Delta APB_1$ and $\Delta APC_1.$ Define $B_a,$ $B_c,$ $C_a,$ $C_b$ cyclically.

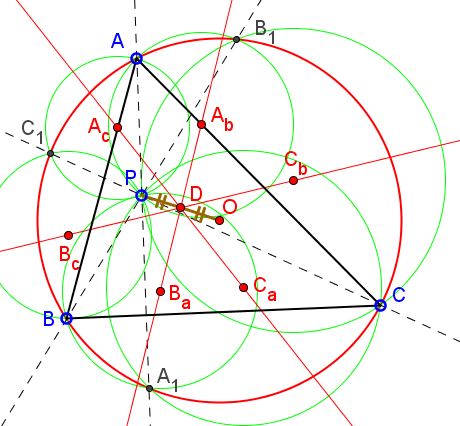
Prove that $A_bB_a,$ $B_cC_b,$ and $A_cC_a$ are concurrent at a point, say $D,$ half way between $P$ and $O.$

Solution

The solution is based on the Isosceles Trapezoid lemma. As seen on the diagram and has been shown in the proof of the lemma, the quadrilateral $OB_cPC_b$ is a parallelogram:

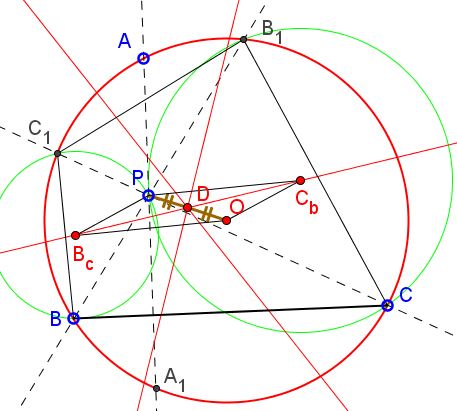
Yet Another Seven Circles Theorem

It follows that $B_cC_b$ and $OP$ intersect at their midpoints. The same holds for $A_bB_a$ and $A_cC_a$ and, so all four segments concur at a their shared midpoint.

Acknowledgment

The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page; Dao Thanh Oai observed that the credit should go to Leonard Giugiuc (Romania) because of the central role his proof of the Isosceles Trapezoid lemma played in the proof of the present statement.

72395393