Isosceles Trapezoid In Cyclic Quadrilateral
What Might This Be About?
Problem
Let $E$ be the intersection of the diagonals $AD$ and $BC$ of the cyclic quadrilateral $ABDC$ inscribed in circle $(O).$ Circles $(AEB)$ and $(CED)$ meet again at $F.$ Denote $H,$ $I$ the circumcenters of $(AEB)$ and $(CED),$ respectively.
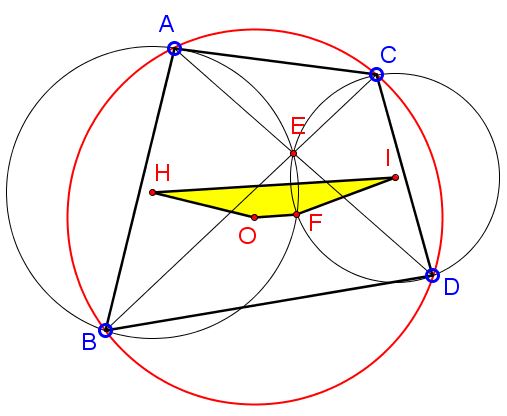
Prove that $FIHO$ is an isosceles trapezoid.
Solution
Triangles $EAB$ and $ECD$ are similar, and so are triangles $HEA$ and $IEC;$ the latter are isosceles with the bases $EA$ and $EC,$ respectively. Let $M$ be the intersection of $IE$ and $AB.$ Then $\angle BEM=\angle CEI;$ $\angle AHE=2\angle MBE,$ such that $\angle BEM+\angle MBE=90^{\circ},$ i.e., $EM\perp AB.$

But also $OH\perp AB,$ making $IE\parallel OH.$ similarly, $HE\parallel OI.$ This makes the quadrilateral $IEHO$ a parallelogram, so the triangles $EHI$ and $OIH$ are congruent. But the triangles $EHI$ and $FHI$ are also congruent,implying that $OIH$ and $FHI$ are congruent, which makes our quadrilateral an isosceles trapezoid.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page; the proof has been supplied by Leonard Giugiuc (Romania).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73599630
