The Devil is in the Exceptions
Problem
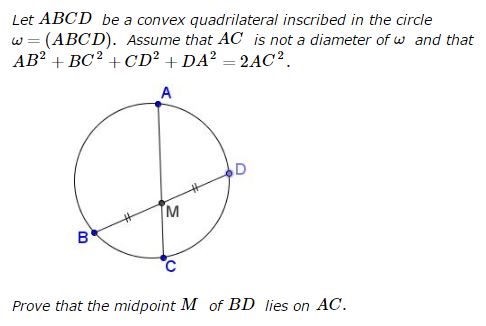
Proof
In triangles $ABC\;$ and $ADC,\;$ $\angle ABC+\angle ADC=180^{\circ}.\;$ Denote $\angle ABC=t.\;$ Note that, since $AC\;$ is not a diameter, $t\ne 90^{\circ}\;$ and, therefore $\cos t\ne 0.\;$ By the Law of Cosines,
$AB^2+BC^2-2\cos t\cdot AB\cdot BC= AC^2,\\ CD^2+DA^2+2\cos t\cdot CD\cdot DA= AC^2.$
Adding the two and dividing by $\cos t,\;$ $AB\cdot BC=CD\cdot DA.\;$ By the sine area formula, $[ABC]=[ADC].$
Let $M=AC\cap BD\;$ and denote $\angle AMB=\angle CMD=\alpha.\;$ We have, $2[ABC]=BM\cdot AC\cdot\sin\alpha\;$ and $2[ADC]=DM\cdot AC\cdot\sin\alpha\;$ from which $BM=DM,\;$ showing that indeed $M\;$ is the midpoint of $BD.$
Exceptional Case
Note that if $AC\;$ is diameter, then the conclusion is not always true. Indeed, if $AC\;$ is a diameter and in $\omega\;$ $AC = 10,\;$ then we can choose $B\;$ on $\omega\;$ such that $AB = 6,\;$ $BC = 8,\;$ and $D\;$ on the other half plane such that $CD = DA = 5\sqrt{2}.\;$

Then clearly $AB^2 + BC^2 + CD^2 + DA^2 = 2AC^2\;$ but the midpoint of $BD\;$ does not belong to $AC\;$ due to the asymmetry of the configuration.
Acknowledgment
Leo Giugiuc has kindly communicated to me a problem form a Romanian Olympics, Grade IX, with a solution.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1966-2016 Alexander Bogomolny73608396
