Tangent Circles, Similarity and Equal Segments
What Might This Be About?
Problem
Let $AB$ be a chord in circle $(O);$ $E$ a point on $AB;$ circles $(O_1)$ and $(O_2)$ - one through $A$ and $E,$ the other through $B$ and $E$ - are tangent to $(O)$ at $A$ and $B,$ respectively. Points $K$ on $(O_1)$ and $L$ on $(O_2)$ satisfy $\angle AEK=\angle BEL.$
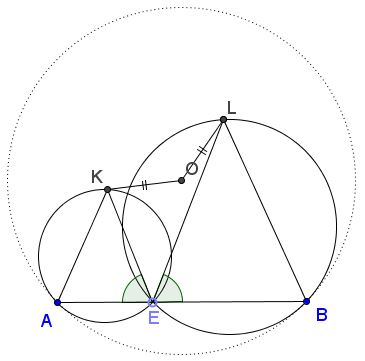
Prove that $OK=OL.$
Solution
First note that triangles $AEK$ and $BEL$ are similar. This is because of the similarity of the three isosceles triangles $AOB,$ $AO_{1}E,$ and $BO_{2}E.$ In particular, $\angle AKE =\angle ELB$ so that the chords $AE$ in $(O_1)$ and $BE$ in $(O_2)$ subtend equal inscribed angles. From the similarity of $AEK$ and $BEL$ we obtain the proportion
(1)
$\displaystyle\frac{EK}{EL}=\frac{AE}{BE}.$
Now, let $L'$ be the second intersection of $EK$ with $(O_1);$ $K'$ the second intersection of $EL$ with $(O_2).$
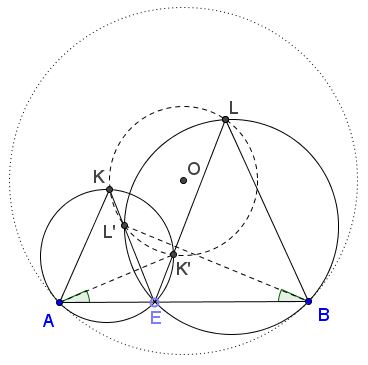
By the above remark, $\angle AK'E=\angle BL'E.$ By the construction, also $\angle AEK'=\angle BEL'.$ This makes triangles $AEK'$ and $BEL'$ similar, implying the proportion
(2)
$\displaystyle\frac{EK'}{EL'}=\frac{AE}{BE}.$
Dividing (1) by (2) yields $EK\cdot EL'=EL\cdot EK',$ which means that the quadrilateral $KL'K'L$ is cyclic.
Let $T$ be the intersection of a perpendicular to $AB$ at $E$ with $(O_1).$ It's not shown in the diagram but try to imagine it there. Then, by the construction, $\angle K'AT =\angle K'ET=\angle KET=\angle KAT.$ Since $\angle AET=90^{\circ},$ $AT$ is a diameter of $(O_1)$ and so triangles $KAT$ and $K'AT$ are right and, thus equal. It follows that $AO_{1} $ passes through $T$ and, as we already knew, through $O.$ Therefore, the perpendicular bisector of $KK'$ passes through $O$ and $O_1.$ Similarly, the perpendicular bisector of $LL'$ passes through $O$ and $O_2$ which ultimately implies that $O$ is the center of $(KL'K'L).$ From here $OK=OL.$
Acknowledgment
This is a slight modification of a problem posted by Dao Thanh Oai at the CutTheKnotMath facebook page. The solution follows up on suggestions by Machó Bónis (Budapest, Hungary).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579598
