Projections of Convex Quadrilateral

Elsewhere I discussed the following problem:

Imagine a pyramid with no symmetries or regularities whatsoever. To construct a pyramid like that, pick a plane, four arbitrary points in the plane and one point outside. The lines (or rays) joining the latter to the four points in the plane serve as the edges of a slanted and likely irregular pyramid. Prove that there is a parallelogram as a cross-section.

At the time, the problem was reduced to planar constructions, interesting and useful in their own right. However, it is hard to miss the fact that the problem is of projective nature: given a convex quadrilateral, is it always possible to project it into a parallelogram? In what follows, the problem is reformulated projectively, with following-up questions answered with Euclidean methods.

We wish to find point $O$ and points $A',$ $B',$ $C',$ $ D'$ on $OA,$ $OB,$ $OC,$ and $OD,$ respectively, such that the quadrilateral $A'B'C'D'$ is a parallelogram.

In a projection, parallel lines either remain parallel or converge at the horizon - the line at infinity. As every other line, the line at infinity is defined by any two of its points. Observe that if we wish to have, say, $A'B'\parallel C'D',$ both need to be parallel to the line joining $O$ with the point at infinity $V=AB\cap CD.$

Similarly, $U=AD\cap BC$ defines another point at infinity, so that $UV$ is to be regarded as the line at infinity, a vanishing line may be a better term in the present context. If we make a projection from an arbitrary point $O$ that takes $UV$ to infinity, then any pencil of lines through, a point on $UV$ will convert to a pencil of parallel lines. This is in particular true for points $U$ and $V.$

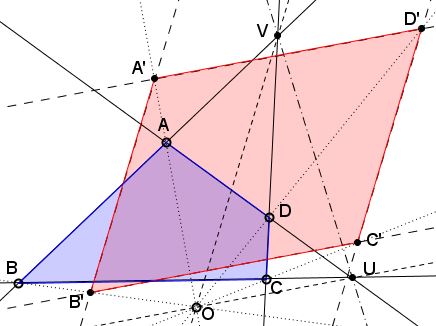
So here is the construction: First determine $U$, $V$ and $UV;$ pick any point $O,$ not on $UV$ and join it to $U$ and $V;$ choose a random point $A'$ on $OA;$ draw $A'B'\parallel OV$ and $A'D'\parallel OU,$ with $B'$ on $OB$ and $D'$ on $OD;$ draw $B'C'\parallel OU,$ with $C'$ on $OC.$ $C'D'$ is bound to be parallel to $OV$ and thus to $A'B'.$

It is also possible to project a given convex quadrilateral into a rectangle, but now the center of projection $O$ has to be chosen more judiciously. Note that, since the side of the parallelogram $A'B'C'D'$ are pairwise parallel to $OU$ and $OV,$ for the parallelogram to become a rectangle we need $OU\perp OV.$

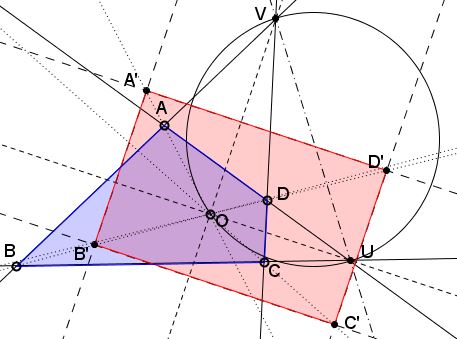
This is achieved with choosing $O$ anywhere on the circle with $UV$ as diameter.

Restricting $O$ even further, it is possible to project $ABCD$ into a square. The rectangle $A'B'C'D'$ will become a square if its two diagonals are perpendicular: $AC\perp BD.$

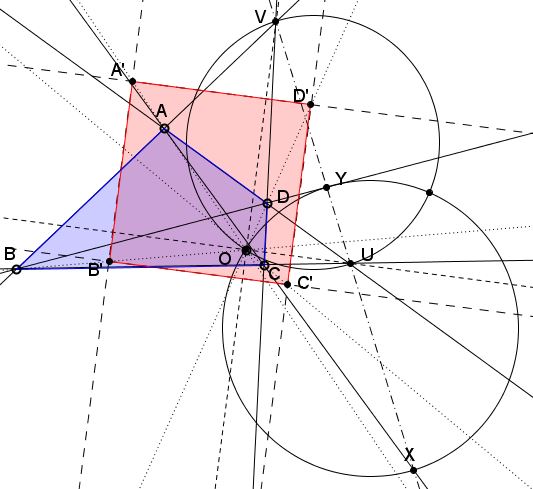
Thus find $X=AC\cap UV$ and $Y=BD\cap UV$ and form a circle with $XY$ as diameter. Setting $O$ at either one of the intersections of the two circles will make $A'B'C'D'$ a square.

C. R. Wylie, Jr., Introduction to Projective Geometry, Dover, 1970, pp 17-20