Proportions and the Incenter
Source
The following problem, due to Miguel Ochoa Sanchez, has been posted by Leo Giugiuc at the CutTheKnotMath facebook page along with a solution (Solution 1) by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.
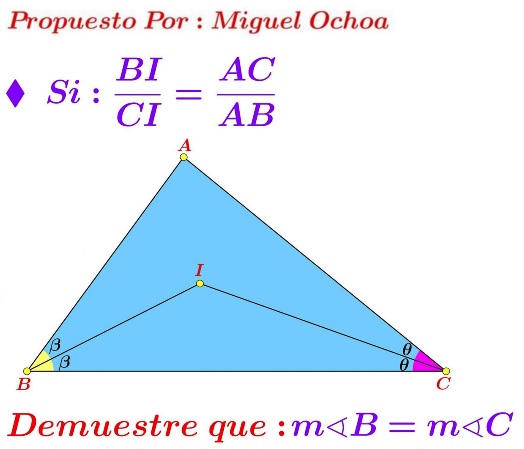
Problem
$I$ is the incenter in $\Delta ABC.$ Prove that $\displaystyle \frac{BI}{CI} = \frac{AC}{AB}\;$ implies $\angle ABC=\angle ACB.$
Solution 1
We know that $\displaystyle BI=\frac{2ac}{a+b+c}\cdot\cos\frac{B}{2}\;$ and $\displaystyle CI=\frac{2ab}{a+b+c}\cdot\cos\frac{C}{2},\;$ implying $\displaystyle\frac{BI}{CI}=\frac{c}{b}\cdot\frac{\cos\frac{B}{2}}{\cos\frac{C}{2}}.$ It follows that $\displaystyle\frac{c}{b}\cdot\frac{\cos\frac{B}{2}}{\cos\frac{C}{2}}=\frac{b}{c},\;$ or $b^2\cdot\cos\frac{C}{2}=c^2\cdot\cos\frac{B}{2}.$
By the Law of Sines,
$\displaystyle 16R^2\cdot\sin^2\frac{B}{2}\cos^2\frac{B}{2}\cos\frac{C}{2}=16R^2\cdot\sin^2\frac{C}{2}\cos^2\frac{C}{2}\cos\frac{B}{2}$
which simplifies to $\displaystyle16\sin^2\frac{B}{2}\cos\frac{C}{2}=\sin^2\frac{C}{2}\cos\frac{C}{2}.\;$
If $B\ne C,$ then $\displaystyle\cos\frac{B}{2}\ne\cos\frac{C}{2}.\;$ Let $\displaystyle\cos\frac{B}{2}=x\;$ and $\displaystyle\cos\frac{C}{2}=y.\;$ We have $(1-x^2)x=(1-y^2)y,\;$ or, $y^3-x^3=y-x.\;$ Since $x\ne y,\;$ this simplifies to $x^2+xy+y^2=1,\;$ or, $xy=1-(x^2+y^2).$
But $0\lt xy$ implies $x^2y^2\lt x^2y^2+xy\;$ and subsequently,
$xy\lt\sqrt{x^2y^2+xy}=\sqrt{x^2y^2+1-(x^2+y^2)}=\sqrt{(x^2-1)(y^2-1)}$
which says that $\displaystyle\cos\frac{B}{2}\cos\frac{C}{2}\lt\sin\frac{B}{2}\sin\frac{C}{2},$ i.e., $\displaystyle\cos\frac{B+C}{2}\lt 0,$ and, finally, $\displaystyle\frac{B+C}{2}\gt\frac{\pi}{2},\;$ which is absurd. Hence, $\displaystyle\cos\frac{B}{2}=\cos\frac{C}{2}\;$ and $B=C.$
Solution 2
Set $\angle ABC=2\beta,$ $\angle ACB=2\theta.$
By the Law of Sines in $\Delta ABC,$ $\displaystyle\frac{AC}{AB}=\frac{\sin 2\beta}{\sin 2\theta}.$ By the Law of Sines in $\Delta IBC,$ $\displaystyle\frac{BI}{CI}=\frac{\sin \theta}{\sin \beta}.\;$ Thus we have
(*)
$\displaystyle \sin 2\beta\cdot\sin \beta=\sin 2\theta\cdot\sin \theta$
from which we should be able to conclude that $\beta = \theta.$ It is clear that we may assume $0\lt\beta,\theta\lt 90^{\circ}.\;$ But on the interval $[0,90^{\circ}]\;$ function $f(x)=\sin 2x\cdot\sin x\;$ is experiencing a hump symmetric in $x=45^{\circ}.$
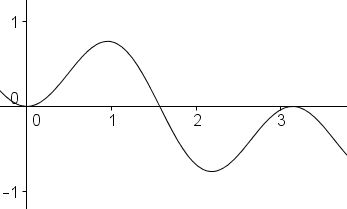
It follows that (*) may only hold when,say, $\beta = 45^{\circ}-\omega$ and $\theta = 45^{\circ}+\omega,$ for $\displaystyle -45^{\circ}\le\omega\le 45^{\circ}.\;$ Thus the only possibility to have $f(\beta)=f(\theta )\;$ is when $\beta+\theta=90^{\circ},$ making $\angle BAC=90^{\circ}.$
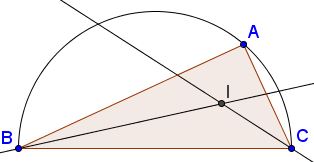
It is now intuitively clear that if $\displaystyle \frac{BI}{CI}\gt 1,\;$ then $\displaystyle\frac{AC}{AB}\lt 1\;$ and vice versa. A rigorous justification makes use of Leo's Lemma.
Assume $0\lt\beta\lt\theta\lt 90^{\circ};\;$ the also $0\lt 2\beta\lt 2\theta\lt 180^{\circ}.\;$ Then $\sin\beta\lt\sin\theta\;$ and, by Leo's Lemma also $\sin 2\beta\lt\sin 2\theta\;$ but then $\displaystyle \frac{BI}{CI} = \frac{AC}{AB}\;$ could not hold. It follows that $\beta=\theta.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581664
