A Property of Nagel Cevians
Source
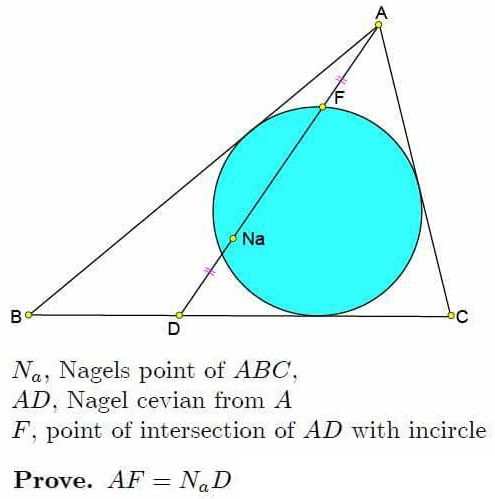
Problem

Lemma
Let $E$ be the point of tangecy of the incircle with $BC.$ Then $FE$ is a diameter of the incircle.
Indeed, draw the excircle $(G)$ opposite $A.$ By definition, $D$ is the point of tangency of $BC$ and $(G).$ If $I$ is the incenter and $(I)$ the incircle, $(G)$ is homothetic to $(I)$ from $A$ with the coefficient $AD/AF.$ Note that $GD\perp BC.$

If $DJ$ is a diameter of $(G)$ then $J$ is the image of $E$ under the homothety. So, it follows that $FE\perp BC,$ making $FE$ a diameter.
Solution
Let $s$ be the semiperimeter of $\Delta ABC$ with the side lengths $a,b,c.$ Introduce $x=s-a,$ $y=s-b,$ $z=s-c.$ Then $a=y+z,$ $b=z+x,$ $c=x+y.$ Since the barycentric coordinates of $I$ are $(a:b:c)=(y+z:z+x:x+y)$ and those of the Nagel point $(s-a:s-b:s-c)=(x:y:z),$ we have (using the above lemma, too):
$\displaystyle\begin{align} \overset{\rightarrow}{AE}&=\frac{z\overset{\rightarrow}{AB}+y\overset{\rightarrow}{AC}}{y+z}\\ \overset{\rightarrow}{AN_a}&=\frac{y\overset{\rightarrow}{AB}+z\overset{\rightarrow}{AC}}{x+y+z}\\ 2\overset{\rightarrow}{AI}&=\frac{(x+z)\overset{\rightarrow}{AB}+(x+y)\overset{\rightarrow}{AC}}{x+y+z}\\ \overset{\rightarrow}{AD}&=\frac{y\overset{\rightarrow}{AB}+z\overset{\rightarrow}{AC}}{y+z}\\ \end{align}$
Since $I$ is the midpoint of $FE$,
$\displaystyle\overset{\rightarrow}{AF}=2\overset{\rightarrow}{AI}-\overset{\rightarrow}{AE}=\frac{x}{x+y+z}\cdot(y\overset{\rightarrow}{AB}+z\overset{\rightarrow}{AC}).$
It follows that $\displaystyle\frac{AN_a}{AF}=\frac{y+z}{x}.$
But, from the van Aubel theorem, $\displaystyle\frac{AN_a}{N_aD}=\frac{y+z}{x}.$
This completes the proof.
Acknowledgment
The problem (by Kadir Altintas) has been posted at the Peru Geometrico facebook group and kindly communicated to me by Leo Giugiuc, along with a solution of his. Additional solutions can be found at the above link.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571460
