Another Concurrence on the 9-Point Circle
What Might This Be About?
Problem
Points $A_1,$ $B_1,$ $C_1,$ and $A_2,$ $B_2,$ $C_2,$ are projections of the vertices of $\Delta ABC$ on two perpendicular lines through the orthocenter $H$ of the triangle.
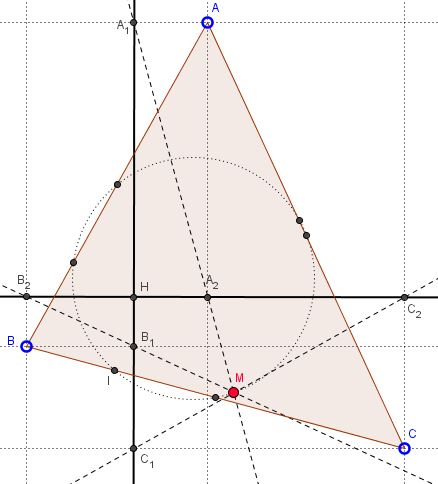
Prove that lines $A_1A_2,$ $B_1B_2,$ $C_1C_2,$ concur on the 9-point circle of $\Delta ABC.$
Hint
If you are after an analytic solution, think of choosing a special coordinate system. There are known to be perpendicular lines, after all.
Solution
Place the origin at the orthocenter $H,$ and let the axes coincide with the given two perpendicular lines. Assume the vertices have the coordinates $A(x_1,y_1),$ $B(x_2,y_2),$ $C(x_3,y_3).$ Then point $(x_i,y_i)$ has projections $(x_i,0)$ and $(0,y_i)$ on the two axes. The line through the two projections is, obviously, $y_i x+x_i y-x_i y_i=0,$ $i=1,2,3.$ The three lines concur iff
$\left| \begin{array}{ccc} y_1 & x_1 & -x_1 y_1 \\ y_2 & x_2 & -x_2 y_2 \\ y_3 & x_3 & -x_3 y_3 \end{array} \right|=0 $
The determinant evaluates to an expression that I prefer to write grouped into three pieces:
(1)
$y_1x_2x_3(y_3-y_2)+x_1y_2x_3(y_1-y_3)+x_1x_2y_3(y_2-y_1).$
Now, the slope of the altitude from $AH$ equals $\displaystyle\frac{y_1}{x_1};$ the slope of $BC$ equals $\displaystyle\frac{y_3-y_2}{x_3-x_2}.$ The product of the two is $-1$ from which
$y_1(y_3-y_2)=-x_1(x_3-x_2).$
Similar identities hold for the other two altitudes. Substituting all three into (1) gives
$x_1x_2x_3(x_3-x_2)+x_1x_2x_3(x_1-x_3)+x_1x_2x_3(x_2-x_1) = 0,$
proving that the three lines indeed concur. It remains to be shown that their common point lies on the 9-point circle.
We may actually solve any two equations that define the straight lines to obtain the coordinates of the common point. The point, say $P,$ has coordinates
$\displaystyle P=\bigg(\frac{x_{1}x_{2}(y_{1}-y_{2})}{y_{1}x_{2}-y_{2}x_{1}},\frac{y_{1}y_{2}(x_{1}-x_{2})}{x_{1}y_{2}-x_{2}y_{1}}\bigg).$
Now, define the Euler points (the points midway between the orthocenter and the vertices) $K(x_{1}/2, y_{1}/2),$ $L(x_{2}/2, y_{2}/2),$ $M(x_{3}/2, y_{3}/2).$ We expect the four points $K,$ $L,$ $M,$ $P$ to be concyclc. Converting to complex variables, this could be verified by checking that the expression
$\displaystyle \frac{P-K}{P-L}:\frac{M-K}{M-L}.$
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page; the proof has been supplied by Leonard Giugiuc (Romania).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73605797
