A Problem in Hinged Squares II

What is this about?

Problem

Given two squares, $AB_1C_1D_1$ and $AB_2C_2D_2.$ Let $O_1$ and $O_2$ be their respective centers. $B_1B_2$ intersects $O_1O_2$ in $B,$ $D_1D_2$ intersects $O_1O_2$ in $D;$ $C$ is the intersection of $B_1B_2$ and $D_1D_2$

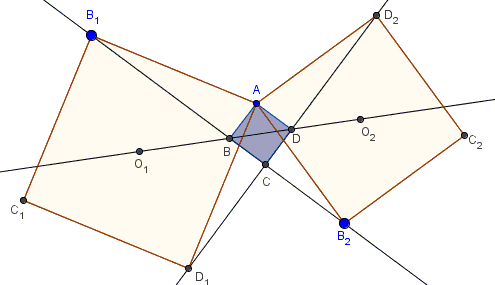
Problem in Hinged Squares II

Prove that $ABCD$ is a square.

Hint

Try to find equal triangles that could be obtained by rotation from each other.

Solution

Triangles $B_1AB_2$ and $D_1AD_2$ are equal and obtained from each other by a rotation around $A$ through $90^{\circ},$ implying that $B_1B_2\perp D_1D_2,$ i.e., $\angle BCD=90^{\circ}.$

Problem in Hinged Squares II - solution

It follows that $C$ lies on the circumcircles of the two given squares and is, therefore, symmetric to $A$ in the line of centers $O_1O_2,$ so that $AB=BC$ and $AD=BD.$

Let $F$ be the midpoint of $D_1B_2.$

Problem in Hinged Squares II - solution, Step 2

In the solution of another problem on hinged squares, it was shown that $FO_1=FO_2,$ $\angle O_1FO_2=90^{\circ},$ and $\angle FO_1O_2=\angle FO_2O_1=45^{\circ}.$ But, say, $FO_1\parallel B_1B_2$ which is $BC.$ Similarly $FO_2\parallel CD$ so that $\angle CBD=45^{\circ},$ implying that $ABCD$ is indeed a square.

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

71921484