Perpendiculars in Parallelogram
What is this about?
Source
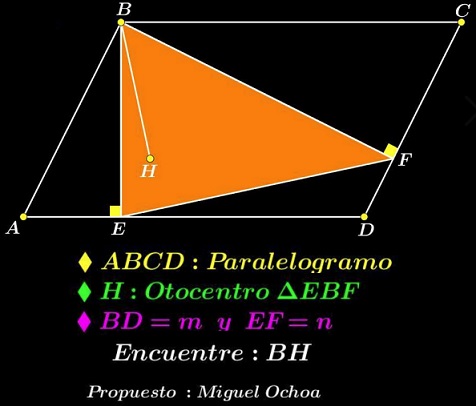
Problem
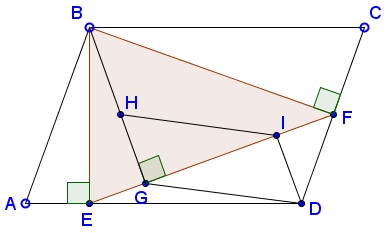
In parallelogram $ABCD,\;$ $E\in AD,\;$ $F\in CD\;$ such that $BE\perp AD\;$ and $VF\perp CD;$ $H\;$ is the orthocenter of $\Delta BEF.$
Let $BD=m\;$ and $EF=m.\;$ Express $BH\;$ in terms of $m\;$ and $n.$
Solution 1
From the diagram, $\Delta ABD\;$ is acute angled. Since $BEDF\;$ is cyclic, we deduce that $\angle EBF=\angle BAE,\;$ implying that that $\Delta EBF\;$ is acute angled. Thus, $BH=2R\cos \angle EBF=m\cos\angle BAE.\;$ We choose $A=(-a,0),\;$ $B=(0,1),\;$ and $D=(b,0),\;$ with $a,b\gt 0\;$ and $ab\lt 1,\;$ from which $E=(0,0).\;$ Further: $DF\;$ is defined by the equation $x-ay=b,\;$ $BF\;$ by the equation $ax+y=1.\;$ $F\;$ is then expressed as $\displaystyle F=\left(\frac{a+b}{a1+a^2}, \frac{1-ab}{1+a^2}\right)\;$ so that $\displaystyle EF^2=\frac{1+b^2}{1+a^2}=\frac{m^2}{1+a^2},\;$ making $\displaystyle a=\frac{\sqrt{m^2-n^2}}{n}.$
Since in $\Delta BAE,\;$ $\displaystyle\cos\angle BAE=\frac{AE}{AB},\;$ we see that
$\displaystyle BH=m\cos\angle BAE=m\cdot\frac{\sqrt{m^2-n^2}/n}{m/n}=\sqrt{m^2-n^2}.$
Solution 2
Observe that quadrilateral $BEDF\;$ is cyclic because angles at $B\;$ and $F\;$ are right. Let $P\;$ be the intersection of $BC\;$ and $(BEDF).\;$ Then $BP\parallel FH\;$ because both are perpendicular to $BE.\;$ Also $FP\parallel BH\;$ because both are perpendicular to $EF\;$ (the latter since $EP\;$ is another diameter of $(BEDF),\;$ $\angle EBP\;$ being right. Thus $BHFP\;$ is a parallelogam. In particular, $BH=FP.\;$
In $\Delta EFP,\;$ $FP=EF\cdot\cot\angle EPF,\;$ which is the same as $BH=EF\cdot\cot\angle EBF=n\cdot\cot\angle EBF.$
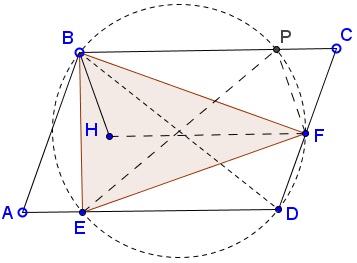
Let $\angle BAD=\alpha,\;$ then also $\angle EPF=\angle EBP=\alpha.\;$ Let $AE=a\;$ and $BE=b.\;$ Then $\displaystyle\cot\alpha =\frac{a}{b}.\;$ Triangles $ABD\;$ and $BEF\;$ are similar so that $\displaystyle\frac{m}{n}=\frac{\sqrt{a^2+b^2}}{b}.\;$ From that, $\displaystyle\frac{a^2}{b^2}=\frac{m^2-n^2}{n^2}.\;$ On the other hand, as we found, $BH=n\cdot\cot\angle\alpha\;$ and $\displaystyle\cot\alpha =\frac{a}{b},\;$ implying $\displaystyle\frac{BH^2}{n^2}=\frac{a^2}{b^2}.\;$ Finally, $BH^2=m^2-n^2.$
Solution 3
Quadrilateral $BEDF\;$ is cyclic, with $BD=m\;$ as a diameter. Thus its radius $\displaystyle R=\frac{m}{2}.$
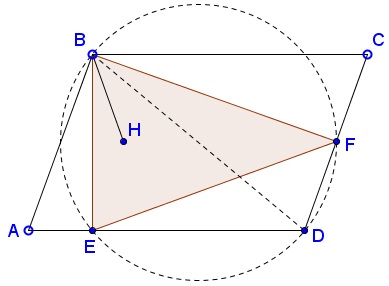
Elsewhere we established a formula: in $\Delta BEF,\;$ $BH^2=4R^2-EF^2\;$ which is $BH^2=m^2-n^2.$
Solution 4
This is a simplification of Solution 2.
Quadrilateral $BEDF\;$ is cyclic, with $BD=m\;$ as a diameter. Let $P\;$ be the intersection of $BC\;$ and $(BEDF).\;$ Then since $\angle EBP=90^{\circ},\;$ $EP$ is another diameter of $(BEDF)\;$ such that $EP=BD=m.\;$

In the right $\Delta EFP,\;$ $EF=n\;$ and $EP=m.\;$ By the Pythagorean theorem, $BH=FP=\sqrt{m^2-n^2}.$
Extra
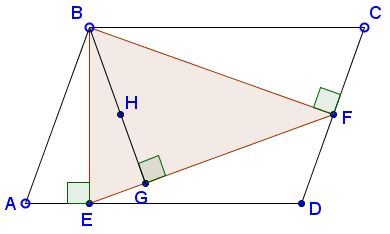
If $G,I\in EF,\;$ with $BG\perp EF\;$ and $DI\perp EF\;$ then $DI=GH.$
Acknowledgment
Leo Giugiuc has kindly posted a problem due to Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. Solution 1 is by Leo Giugiuc and Dan Sitaru; Solution 2 by Ali Naim Geylani.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573603
