Pentagon And Decagon, Both Regular
Source
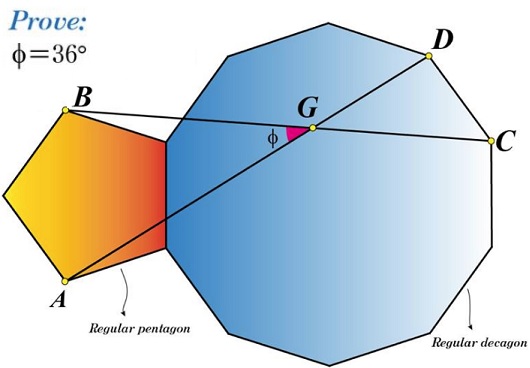
The problem has been brought to my attention by Leo Giugiuc who linked it at the CutTheKnotMath facebook page from the The School Yard Olympiad facebook group. The problem has been originally posted by Kadir Altintas.
The problem could be solved in complex numbers by the method Leo Giugiuc used to solve earlier a similar problem. Like in that case, one could expect the diagram to have many interesting properties. Indeed, playing with GeoGebra, I came across a few. So, instead of solving the problem, I offer my findings below that may be construed as a sequence of additional problems waiting resolution.
Problem
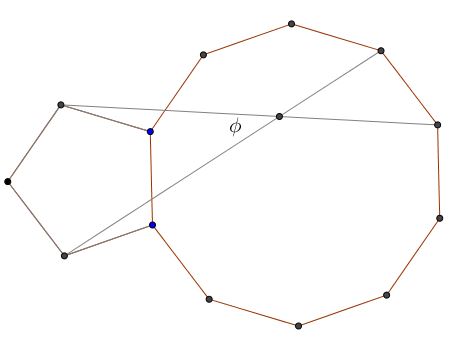
Solution
Solution is by Amit Itagi.
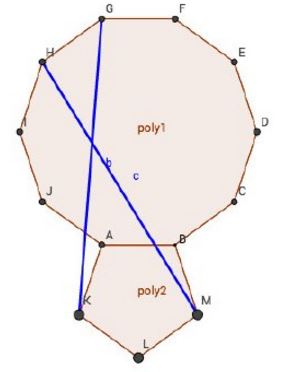
Let the sides of the polygons be of length $l$. Treating the plane as the complex plane with $0$ at point B, the complex values of the points are given by
$\displaystyle \begin{align} G&=l[e^{i\theta}+e^{2i\theta}+e^{3i\theta}+e^{4i\theta}+e^{5i\theta}] \\ H&=l[e^{i\theta}+e^{2i\theta}+e^{3i\theta}+e^{4i\theta}+e^{5i\theta}+e^{6i\theta}] \\ M&=le^{-2i\theta} \\ K&=l[e^{-2i\theta}+e^{-4i\theta}+e^{-6i\theta}] \end{align}$
where $\theta=\frac{\pi}{5}$. Note, $e^{5i\theta}=e^{-5i\theta}=-1$. The required angle is the argument of
$\displaystyle \begin{align} Z&=\frac{H-M}{G-K} \\ &=\frac{e^{i\theta}+e^{2i\theta}+e^{3i\theta}+e^{4i\theta}+e^{5i\theta}+e^{6i\theta}-e^{-2i\theta}}{e^{i\theta}+e^{2i\theta}+e^{3i\theta}+e^{4i\theta}+e^{5i\theta}-e^{-2i\theta}-e^{-4i\theta}-e^{-6i\theta}} \\ &=\frac{e^{i\theta}+e^{2i\theta}+e^{3i\theta}+e^{4i\theta}-1-e^{i\theta}+e^{3i\theta}}{e^{i\theta}+e^{2i\theta}+e^{3i\theta}+e^{4i\theta}-1+e^{3i\theta}+e^{i\theta}-e^{4i\theta}} \\ &=\frac{e^{2i\theta}+2e^{3i\theta}+e^{4i\theta}-1}{2e^{i\theta}+e^{2i\theta}+2e^{3i\theta}-1} \end{align}$
$\displaystyle \begin{align} \frac{Z}{Z^*}&=\left(\frac{e^{2i\theta}+2e^{3i\theta}+e^{4i\theta}-1}{2e^{i\theta}+e^{2i\theta}+2e^{3i\theta}-1}\right)\left(\frac{2e^{-i\theta}+e^{-2i\theta}+2e^{-3i\theta}-1}{e^{-2i\theta}+2e^{-3i\theta}+e^{-4i\theta}-1}\right) \\ &=\left(\frac{e^{2i\theta}+2e^{3i\theta}+e^{4i\theta}-1}{2e^{i\theta}+e^{2i\theta}+2e^{3i\theta}-1}\right)\left(\frac{2e^{4i\theta}+e^{3i\theta}+2e^{2i\theta}+1}{e^{3i\theta}+2e^{2i\theta}+e^{i\theta}+1}\right) \\ &=\frac{e^{4i\theta}-e^{3i\theta}-6e^{2i\theta}-6e^{i\theta}-6}{6e^{4i\theta}+6e^{3i\theta}+e^{2i\theta}-e^{i\theta}-6} \\ &=\frac{e^{2i\theta}(e^{2i\theta}-e^{i\theta}-6-6e^{-i\theta}-6e^{-2i\theta})}{6e^{4i\theta}+6e^{3i\theta}+e^{2i\theta}-e^{i\theta}-6} \\ &=\frac{e^{2i\theta}(e^{2i\theta}-e^{i\theta}-6+6e^{4i\theta}+6e^{3i\theta})}{6e^{4i\theta}+6e^{3i\theta}+e^{2i\theta}-e^{i\theta}-6} \\ &=e^{2i\theta} \end{align}$
Thus, $arg(Z)=\theta=\pi/5=36^o$.
Observation 1
First off, there is a whole bunch of equal angles subtended by the same diagonal of the pentagon. There is, therefore, a circle through multiple points of intersection of the segments joining vertices of the two polygons.
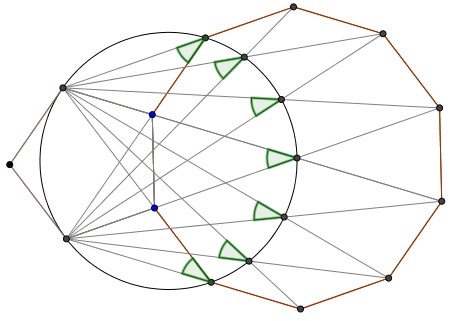
The two angles at the extremes are obviously $36^{\circ}.$
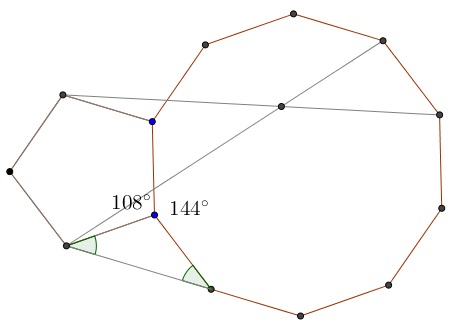
Observation 2
There is a hyperbola through some of the points of intersection:

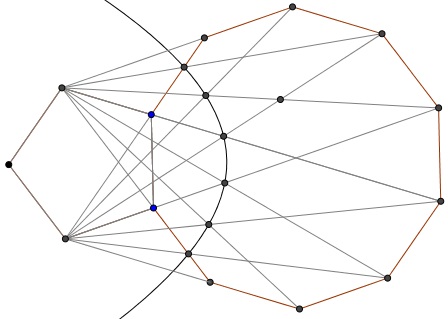
Observation 3
There is another hyperbola through some other points of intersection:
Observation 4
In a configuration of a pentagon and decagon, one would expect to encounter the Golden Ratio. Indeed, I found one:
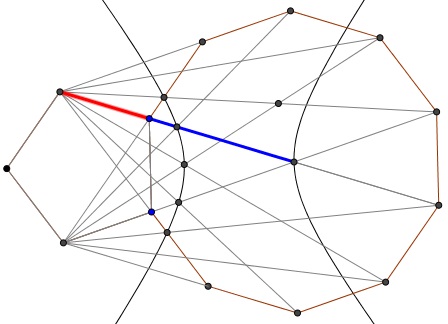
and then another one:
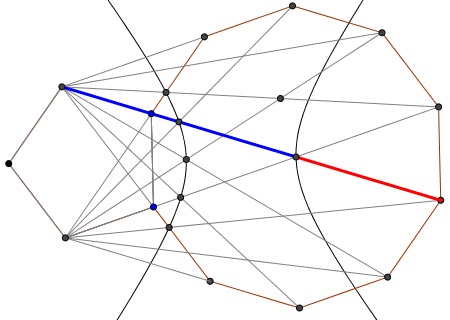
and a couple more:
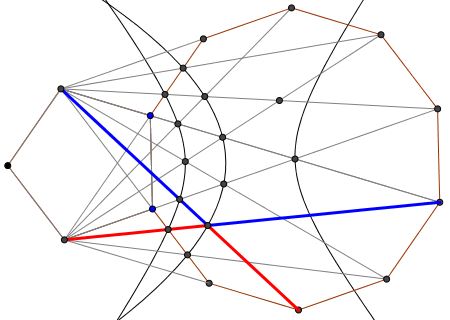
Perhaps there are more.
Observation 5
Kadir Altintas has observed that two of the segments joining the vertices of the two polygons pass through the center of the decagon and that each of these divides two other pairs in the ratio $1:1.$
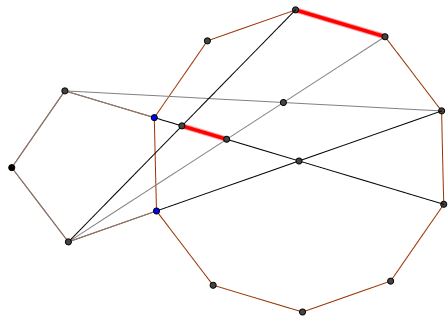
Efthymis Alexiou has provided a proof:
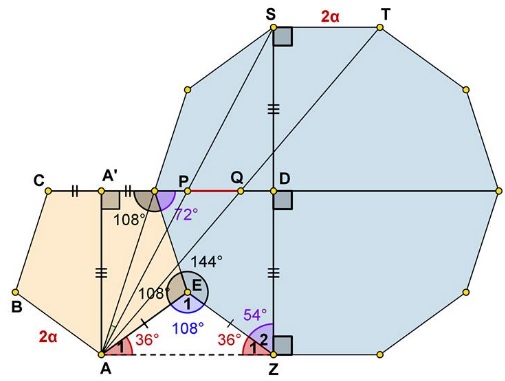
$\displaystyle \begin{align} &\angle E_1=360^{\circ}-108^{\circ}-144^{\circ}=108^{\circ}\,\Longrightarrow\\ &\angle A_1=\angle Z_1=\frac{180^{\circ}-108^{\circ}}{2}=36^{\circ}\,\Longrightarrow\\ &\angle Z_1+Z_2=36^{\circ}+54^{\circ}=90^{\circ}\,\Longrightarrow\\ &AZ\perp DZ\,\Longrightarrow\,AA'=ZD=DS\,\Longrightarrow\,P,Q\,\text{divide}\,AS,AT,\,\text{respectively}. \end{align}$
It follows hat $\displaystyle PQ=\frac{ST}{2}.$
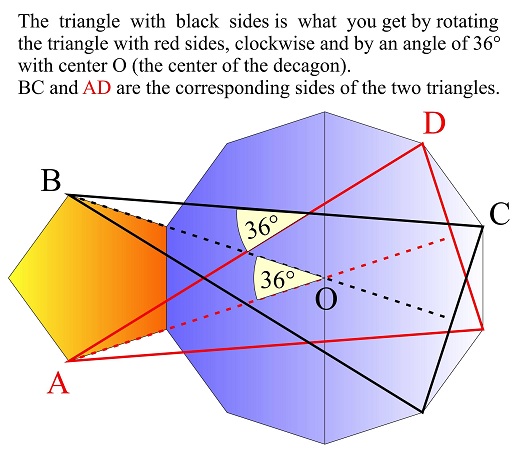
Observation 6
John Arioni solved the problem in a most elegant way.
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582386
