Pedal Parallelogram
What Might This Be About?
Problem
This is the question posed by Emil Stoyanov in a comment to another page.
Given $\Delta ABC$ and point $D$ within the triangle. Let $M,$ $N,$ $P,$ be the pedal points of point $D.$
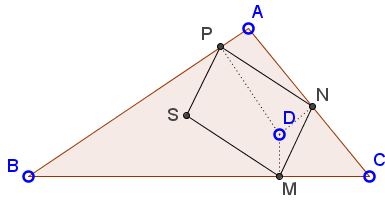
Then there exists point $S$ within $\Delta ABC$ such that the four points $M,$ $N,$ $P,$ and $S$ form a parallelogram.
Proof
Construct $\Delta M'N'P'$ for which $\Delta MNP$ serves the medial triangle.
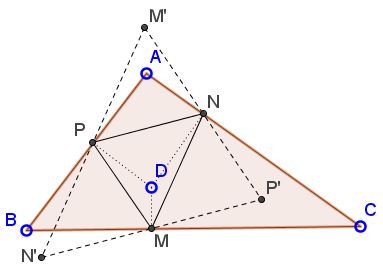
There are three parallelograms with vertices $M,$ $N,$ $P:$ $MNPN',$ $NPMP',$ and $PMNM'.$ Thus the problem will be solved if we prove that one of the points $M',$ $N',$ $P',$ lies within $\Delta ABC.$
There is point $A'$ on $BC$ such that, for $D=A',$ $NP\parallel BC.$ This remains so for all $D\in AA'.$ When this happens both $N'$ and $P'$ lie on the side line $BC.$ Denote this side line $\alpha.$
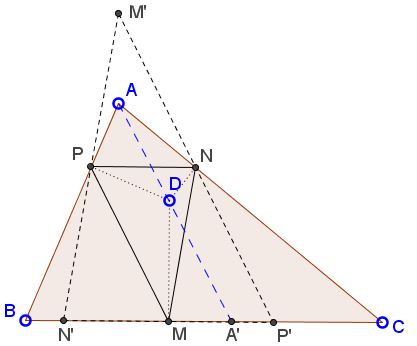
Except for the case $D\in AA',$ points $N'$ and $P'$ lie on different sides of line $\alpha.$ Clearly, $N'$ and $P'$ cannot lie on the same side of $\alpha$ because $N'P'$ crosses $\alpha$ at $M.$ Moreover, one of $N'$ or $P'$ that lies on the same side of $AA'$ as $D,$ lies on the side of $\alpha$ opposite $A.$ (In the diagram below this is $N'),$ while $P'$ lies on the same side of $\alpha$ as $A.$
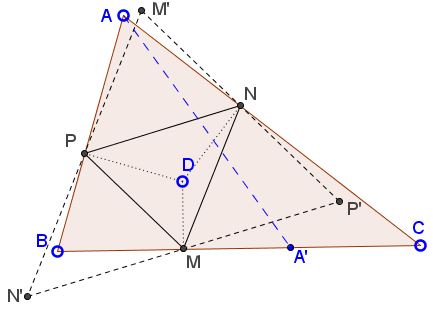
This is because sliding $M$ away from $A'$ towards, say, $B$ pushes $P$ down $AB$ and $N$ up $AC.$ Relative to $\alpha$ the movement of $N'$ and $P'$ is opposite to that of $N$ and $P,$ respectively.
In general, the endpoints of the segments $M'N',$ $N'P',$ and $P'M'$ are on different sides of relevant side lines and cross in and out of $\Delta ABC$ at points $P,$ $M,$ and $N,$ respectively. We can see that all three points $M',$ $N',$ $P'$ cannot be outside $\Delta ABC.$
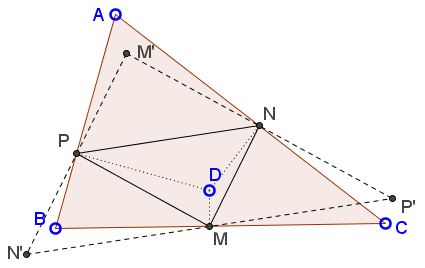
Indeed, assume that, say, $N'$ and $P'$ are outside. Then lines $N'M'$ and $P'M'$ cross at $P$ and $N$ from outside inside, implying that they also meet (at point $M')$ inside $\Delta ABC$ ($\Delta APN,$ actually.)
Note 1: Point $A'$ is the foot of the cevian through the circumcenter $O$ of $\Delta ABC.$ This is because The lines joining the feet of the altitudes are antiparallel and the circumcenter is the isogonal conjugate of the orthocenter.
Note 2: An absolutely analogous behavior is observed when $AM,$ $BN,$ $CP$ are the cevians through $D.$ This is discussed on a separate page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73584237
