Parallelogram in Four Circles
What is this about?
Problem
Given four congruent concurrent circles $(A),$ $(B),$ $(C),$ $(D)$ that meet second time in successive points $E,F,G,H.$
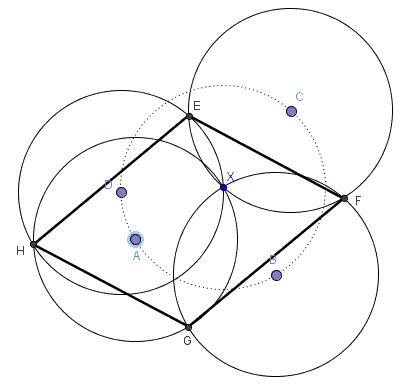
Prove that $EFGH$ is a parallelogram
Hint
Pressing the Hint button may help observe additional parallelograms.
Solution
For a proof, consider an abridged diagram:
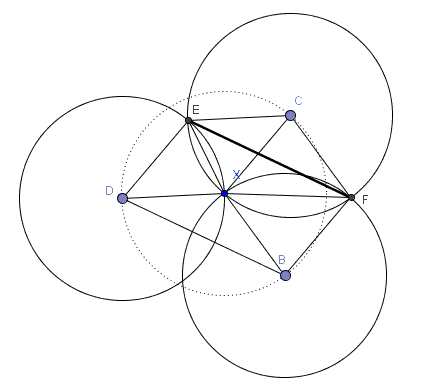
$X$ is the common point. I wish to prove that $BD$ is parallel and equal to $CE.$
$BFCX$ is a rhombus because all its sides equal the common radius of the given circles. $CDEX$ is also a rhombus for exactly same reason. Thus, $BX||FC$ and $DX||EC.$\( \begin{align} \angle BXD &= 360^{\circ} - \angle BXF - \angle CXF -\angle DXE - \angle EXC \\ &= (180^{\circ} - \angle CFX -\angle CXF) - (180^{\circ} - \angle CEX -\angle CXE) \\ &= \angle ECX + \angle FCX \\ &= \angle ECF. \end{align} \)
It follows (by SAS) that $\Delta BDX=\Delta FCE,$ with two pairs of parallel sides, making the third pair parallel (and, of course equal.)
Now, in the same manner, $BD||GH$ and $BD=GH$. By the transitivity of the property of being parallel and that of being equal, $EF||GH$ and $EF=GH$ as required.
Acknowledgment
This problem was posted at the CutTheKnotMath facebook page by Dao Thanh Oai.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581469
