Orthogonal Lines, Midpoints, and Collinearity
What Might This Be About?
Problem
Let two perpendicular lines pass through the orthocenter $H$ of $\Delta ABC.$ Assume they meet the sides $AB$ and $AC$ in $C_1,B_1$ and $C_2,B_2,$ respectively. Define $M_i$ as the midpoint of $B_{i}C_{i},$ $i=1,2,$ and $M$ the midpoint of $BC.$
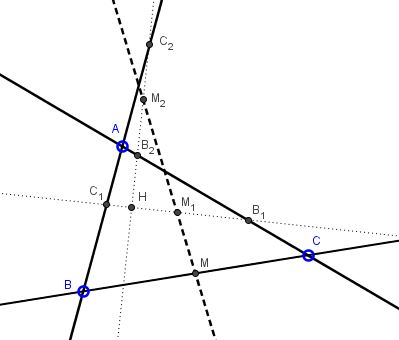
Prove that $M_{1},$ $M_{2}$ and $M$ are collinear.
Solution
As has already been done previously, we choose to place the origin of the coordinate system at the orthocenter and the axes along the two given lines. We thus may specify the coordinates of the points involved: $C_{1}(2a,0),$ $C_{2}(2b,0),$ $B_{1}(2c,0),$ $B_{2}(2d,0),$ $B(2x_{1},2y_{1}),$ $C(2x_{2},2y_{2}).$ Given that, the midpoints can be found: $M_{1}(a+c,0),$ $M_{2}(0,b+d),$ $M(x_{1}+x_{2},y_{1}+y_{2}).$ Next come the equations of the straight lines. $B_{1}B_{2}:\space dx+cy=2cd$ and $C_{1}C_{2}:\space ax+by=2ab.$
Since $B$ is on $C_{1}C_{2}$ and $C$ on $B_{1}B_{2},$ we get
(1)
$ax_{1}+by_{1}=2ab$ and $dx_{2}+cy_{2}=2cd.$
Collinearity of the three midpoints is equivalent to
$\left|\begin{array}{ccc} a+c & 0 & 1 \\ 0 & b+d & 1 \\ x_{1}+x_{2} & y_{1}+y_{2} & 1 \end{array}\right|=0, $
which, using (1), reduces to
(2)
$ad+bc=dx_{1}+bx_{2}+cy_{1}+ay_{2}.$
Finally, since $BH\perp AC,$ the product of the slopes of the two lines is $-1$ and so $cx_{1}-dy_{1}=0$ and, similarly, $ax_{2}-by_{2}=0.$ Now for each pair $(x_{1},y_{1}$ and $(x_{2},y_{2}$ we have a system of two linear equations, solving which gives: $\displaystyle x_{1}=\frac{abd}{ac+bd},$ $\displaystyle y_{1}=\frac{abc}{ac+bd},$ $\displaystyle x_{2}=\frac{bcd}{ac+bd},$ $\displaystyle y_{2}=\frac{acd}{ac+bd}.$ Substituting the four into (2) immediately verifies (1) and, thus the collinearity of the midpoints.
Note: it is easy to verify with GeoGebra that $H$ is not a unique point with this property.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page; the proof has been supplied by Leonard Giugiuc (Romania).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73576819
