Surprising Length Dependence In Equilateral Triangle by Miguel Ochoa Sanchez
Source

Problem
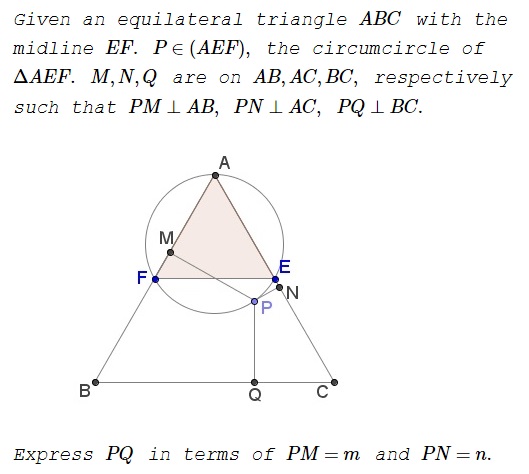
Solution 1
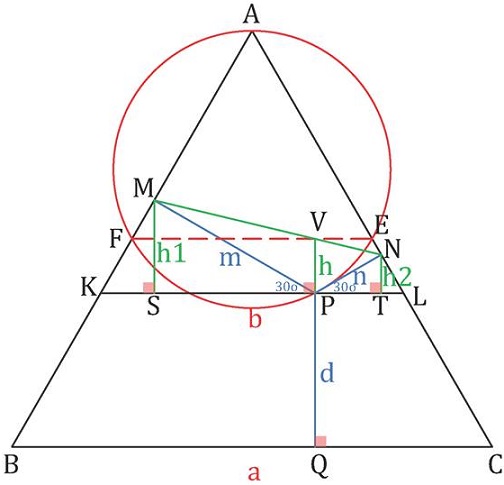

Solution 2
Let the actual distance trilinear coordinates of point $P$ be $(m,n,l)$ and $(m,n,p)$ with respect to the triangles $AEF$ and $ABC$, respectively.
From the equation of the circumcircle of an equilateral triangle in trilinear coordinates (for $AEF$), we have
$mn+nl+lm=0.$
In any equilateral triangle, the trilinear coordinates $(x,y,z)$ satisfy $a(x+y+z)=2S,\,$ where $a$ is the side and $S$ is the area. Noting that $\displaystyle\frac{S}{a}$ for $ABC$ is twice that for $AEF$.
$(m+n+p)=2(m+n+l).$
Eliminating $l$ from the two equations,
$\displaystyle p=\frac{m^2+n^2}{m+n}.$
Solution 3
Let $Q'\,$ be the intersection of $MN\,$ and $QP.\,$ Then the quadrilaterals $ENPQ'\,$ and $FMQ'P\,$ are cyclic; $\angle EPF=120^{\circ}=\angle MPN.\,$ For every point $X\,$ on the arc $EPN\,$ of $(ENPQ'),\,$ the second intersection $Y\,$ of $XQ'\,$ with $(FMQ'P)\,$ has the property that $XPY=120^{\circ},\,$ implying that $MN\,$ passes through $Q'\,$ for an assumption to contrary leads to a contradiction.
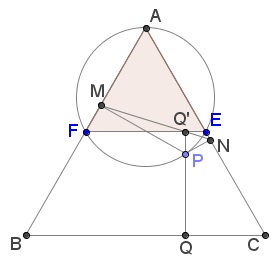
It follows that $PQ'\,$ is the bisector of angle at $P\,$ in $\Delta MNP,\,$ from which we conclude that $\displaystyle PQ'=\frac{mn}{m+n}.$
Assuming, WLOG, $AB=4\,$ we have $QQ'=\sqrt{3}\,$ and, according to Viviani's theorem, $m+n+PQ=2\sqrt{3}.\,$ Since also $\displaystyle \sqrt{3}-\frac{mn}{m+n}=PQ,\,$ we have
$\displaystyle (m+n+PQ)+2\left(\sqrt{3}-\frac{mn}{m+n}\right)=2\sqrt{3}+2\cdot PQ,$
from which $\displaystyle PQ=m+n-2\frac{mn}{m+n}=\frac{m^2+n^2}{m+n}.$
Acknowledgment
This is a problem by Miguel Ochoa Sanchez that was posted at the Peru Geometrico facebook group. Solution 1 is by Thanos Kalogerakis; Solution 2 is by Amit Itagi.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581665
