Euler Line through a Vertex

Source

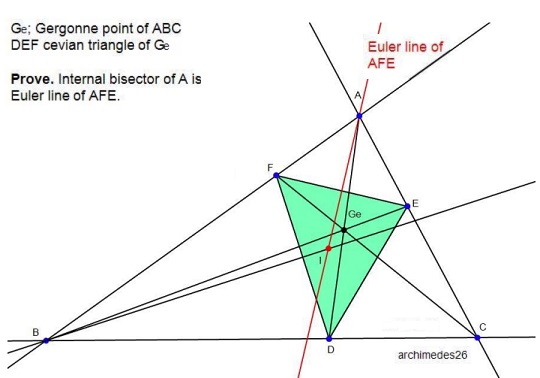
Problem

$DEF$ is a cevian triangle of Gergonne's point $G_e$ in $\Delta ABC.$

Prove that the internal angle bisector of A is the Euler line of $\Delta AFE.$

Solution

Let $a=y+z,$ $b=x+z,$ $c=x+y.$ We have $E=(z,0,x)$ and $F=(y,x,0),$ from which the centroid of $\Delta AEF,$ is

$G_{\Delta AEF}=(k,x(x+z),x(x+y))$

for some $k.$ Also,

$I=I_{\Delta ABC}=(y+z,x+z, x+y).$

So that

$\left|\begin{array}{ccc}1&0&0\\k&x(x+z)&x(x+y)\\y+z&x+z&x+y\end{array}\right|=0,$

It follows that $G_{\Delta AEF}\in OI,$ but clearly $O_{\Delta AEF}\in AI,$ and we are done.

Acknowledgment

This porblem by Kadir Altintas has been kindly communicated to me by Leo Giugiuc, along with a soltion of his; the problem previuosly posted at the Peru Geometrico facebok group.

71946128